Home
Class 12
PHYSICS
Prove the following formula when refract...

Prove the following formula when refraction takes place at a convex spherical refracting surface and source of light lies in the rarer medium and image formed is real `frac(mu_2)(v)-frac(mu_1)(u)=frac(mu_2-mu_1)(R)` Where the terms have their usual meanings.

Text Solution

Verified by Experts

Assumptions: (i) The object is a point object and lying on the principal axis.
(ii) The aperature of refracting spherical surface is small.
(iii) The incident ray, refracted ray and normal make smaller angles with principal axis.
Cartesian sign conventions,
(i) All the distances are measured from the pole of the spherical surface.
(ii) The distances measured along the incident ray are taken as positive and distances measured opposites to direction of incident ray are taken as negative.
(iii) The distances measured in vertically upward direction from principal axis are taken as positive and in vertically downward direction from principal axis are taken as negative.
Consider a convex spherical refracting surface of refractive index `mu_(2)`. Let it be placed in a rarer medium of refractive index `mu_(1)(mu_(2)gtmu_(1))`.
A point object O lies on the principal axis at a distance u from the pole of the convex refracting surface in rarer medium. A ray of light from O incident the convex surface at A. AC is the normal to the convex surface. After refraction at A, the ray enters the dense medium and bends towards the normal. The refracted ray meets the principal axis at I which is the real image of the object O. The distance of the image I from the pole of the convex surface is V.

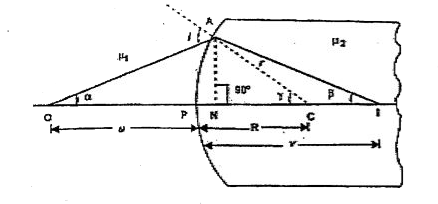
d Let `alpha, beta` and `gamma` be the angles made by the incident ray, refracted ray and the normal respectively with the principal axis. Draw AN perpendicular on the principal axis.
From `DeltaAOE" "i=alpha+gamma`.............i
Since `alpha, beta` and `gamma` are small angles (assumption) so they can be replaced by their tangents,
Hence eqn (i) becomes
`i=tanalpha+tangamma`................ii
From `DeltaAIC" "gamma=r +beta" "or" "r=gamma-beta`...........iii
Again `gamma` and `betas` are small (assumption) so they can be replaced by their tangents. HEnce eq (iii) becomes
`r=tan gamma-tan beta` ............iv
Determination of `tan alpha, tan beta` and `tan gamma`
From rt. `/_d DeltaANO" "tan alpha=(AN)/(NO)`............v
From rt. `/_d DeltaANC, " "tan gamma=(AN)/(NC)`..........vi
From rt. `/_d DeltaANI" "tan beta=(AN)/(NI)`.............vii
Using eqns v to vi we can writes eqn (iii) and (iv) as
`i=(AN)/(NO)+(AN)/(NC)`......................viii and `r=(AN)/(NC)-(AN)/(NI)`..........ix
Since aperture of the spherical surface is small (assumption) so point N lies very close to point P.
`:.NO=PO,NC~=PC` and `NI~=PI`
Hnece eqn viii and ix can be written as
`i=(AN)/(PO)+(AN)/(PC)`.........x
and `r=(AN)/(PC)-(AN)/(PI)` ...........xi
Now according to Snell.s law
`(sini)/(sinr)=(mu_(2))/(mu_(1))` or`mu_(1)sini=mu_(2)sinr`
`:.i` and r are small angles
so sin i=i and sin r=r
`impliesmu_(1)i=mu_(2)r`
Using eqns (x) and (xi)
`mu_(1)[(AN)/(PO)+(AN)/(PC)]=mu_(2)[(AN)/(PI)-(AN)/(PC)]`
`implies(mu_(1))/(PO)+(mu_(1))/(PC)=(mu_(2))/(PI)-(mu_(2))/(PC)`.....xii
Applying sign conventions
`PO=-u,PC=R,PI=-v`
From eqn xii
`(mu_(1))/(-u)+(mu_(1))/R=(mu_(2))/(-v)+(mu_(2))/R`
`implies-(mu_(1))/u+(mu_(2))/v=(mu_(2))/R-(mu_(1))/R`
`-(mu_(1))/u+(mu_(2))/v=(mu_(2)-mu_(1))/R`
Divide all the terms on both sides by `mu_(1)` we have `-1/u+(mu_(2)//mu_(1))/v=(mu_(2)//mu_(1)-1)/R`
But `(mu_(2))/(mu_(1))=""^(1)mu_(2)=mu=` Refractive index of medium 2 w.r.t medium 1.
`implies-1/u-(mu)/v=(mu-1)/R`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • REFRACTION OF LIGHT

    BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS|36 Videos

  • REFRACTION OF LIGHT

    BETTER CHOICE PUBLICATION|Exercise SHORT ANSWER TYPE QUESTIONS|19 Videos

  • REFLECTION OF LIGHT

    BETTER CHOICE PUBLICATION|Exercise NUMERICALS PROBLEMS|7 Videos

  • SEMI CONDUCTOR DEVICES

    BETTER CHOICE PUBLICATION|Exercise Most Expected Questions|6 Videos

Similar Questions

Explore conceptually related problems

Stating new cartesian sign conventions, derive the relation -n_(1)/u+n_(2)/v=(n_(2)-n_(1))/R . Or Prove that when refraction takes place from rarer to denser medium at a convex spherical refracting surface -n_(1)/u+n_(2)/v=(n_(2)-n_(1))/R , where letters have their usual meanings. Or Prove the following formula when refraction takes place at a convex spherical refracting surface and source of light lies in the rarer medium and image formed is real. n_(2)/v=n_(1)/u=(n_(2)-n_(1))/R , where the the terms have their usual meanings. Or Derive the expression -n_(1)/u+n_(2)/v=(n_(2)-n_(1))/R . when the refraction occurs from rarer to denser medium at convex spherical refracting surface (n_(1)

Prove the followign formula when refraction takes place at a convex spherical refracting surface and source of light lies in the denser medium and image formed is virtual. (mu_(1))/u-(mu_(2))/v=(mu_(1)-mu_(2))/R Where the symbols have their meaning.

Prove the following formula when refraction occurs from rarer to denser medium at a convex spherical refracting surface and image formed is virtual. -(mu_(1))/u+(mu_(2))/v=(mu_(2)-mu_(1))/R

Show that I = (mu_r-1) H , where the symbols have their usual meanings.

Derive expression for the lens maker’s formula i.e.: frac(1)(f)= (mu-1) (frac(1)(R_1)-frac(1)(R_2)) where the letters have their usual meanings

Prove that -n/u+1/v=(1-n)/R . When object lies in denser medium and image formed is virtual.

Stating the sign convensions and assumptions, derive the expression for lens maker's formula in case of double convex lens. OR Derive an expression for lens maker's formula 1/f=(mu-1)(1/(R_(1))-1/(R_(2))) Or Describe lens maker's formula (convex lens). Why is it so called? Or Derive the lens maker's formula for a thin lens by giving the assumptions made. Or State sign conventions and assumption, derive thke expression for the lens maker formula i.e. 1/f=(mu-1)(1/(R_(1))-1/(R_(2))) where the letters have their usual meanings. Or Derive the lens formula for a thin convex lens. Or By giving sing conventions and assumption made, derive lens maker's formula for convex lens. Or With the help of suitable diagram, rign conventions and assumptions, derive lens maker's formula for a convex lens.

Prove that n_(1)/-u+n_(2)/v=(n_(2)-n_(1))/R , when refraction occurs from rarer to denser medium at a concave spherical refracting surface.

For a spherical surface,when refraction takes place from a rarer medium (mu_1) to a denser medium (mu_2) , we write -(mu_1)/u + (mu_2)/v = ( mu_2-mu_1)/R where the symbols have their usual meanings. Now suppose that the object is placed in the denser to the rarer medium . Then, rewrite the above equation.

Using new Cartesian sign conventions, derive -n_(2)/u+n_(1)/v=(n_(1)-n_(2))/R when refraction occurs at convex spherical refracting surface and object lies in denser medium. Or Prove that , -n_(2)/u+n_(1)/v=(n_(1)-n_(2))/R for real image formation, when refraction occurs from denser U VR to rarer medium at a convex spherical refracting surface.

Home
Profile