Column-I gives certain situations involving two thin conducting shells connected by a conducting wire via a key K. In all situation one sphere has net charge +q and other sphere has no net charge. After the key K is pressed, column-II gives some resulting effect.
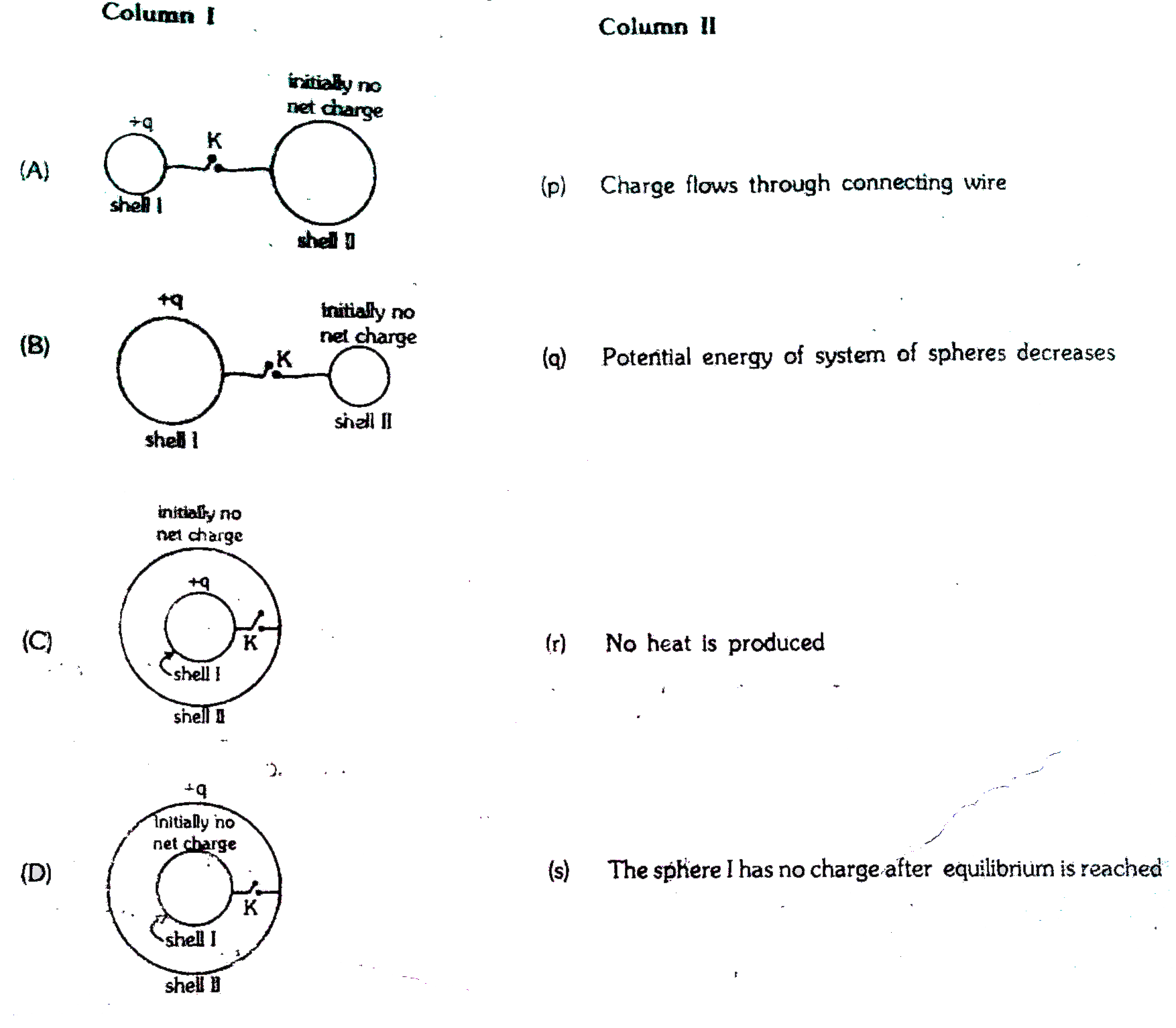
Column-I gives certain situations involving two thin conducting shells connected by a conducting wire via a key K. In all situation one sphere has net charge +q and other sphere has no net charge. After the key K is pressed, column-II gives some resulting effect.


Text Solution
Verified by Experts
The correct Answer is:
(A) p, q (B) p, q (C) p, q s (D) r, s
(A) Initially, the potential difference exist between both shells, so positive charge is flow from high to low potential.
Wvery system wants to acquire minimum potential energy if possible for stability. So charge flown to achieve it.
(B) As explained in [A], charge flow does not depends on the size of sphere.
(C) Charge flow through wire until the potential becomes same for both shells.
(D) Potential is same everywhere inside a conducting shell. So no charge is flow through connecting wire, so no heat is produced.
Wvery system wants to acquire minimum potential energy if possible for stability. So charge flown to achieve it.
(B) As explained in [A], charge flow does not depends on the size of sphere.
(C) Charge flow through wire until the potential becomes same for both shells.
(D) Potential is same everywhere inside a conducting shell. So no charge is flow through connecting wire, so no heat is produced.
Topper's Solved these Questions
MISCELLANEOUS
ALLEN|Exercise Exersice-05|1 VideosMISCELLANEOUS
ALLEN|Exercise Exercise-06|1 VideosMISCELLANEOUS
ALLEN|Exercise Exersice-04|1 VideosKINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
ALLEN|Exercise BEGINNER S BOX-7|8 VideosPHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
ALLEN|Exercise EXERCISE-IV|8 Videos
Similar Questions
Explore conceptually related problems
Column I gives certain situations involving two thin conducting shells connected by a conducting wire via a key K. In all situations, one sphere has net charge +q and other sphere has not net charge. After the key K is pressed, column II gives some resulting effects. Match the figures in Column I with the statement in Column II.
The two conducting spherical shells are joined by a conducting wire and cut after some time when charge stops flowing. Find out the charge on each sphere after that.
The circuit involves two ideal cells connected to a 1 mu F capacitor via a key K. Initially the key K is in position 1 and the capacitor is charged fully by 2V cell. The key is then pushed to position 2. Column I gives physical quantities involving the circuit after the key is pushed from position 1. Column II gives corresponding results. Match the statements in Column I with the corresponding values in Column II. {:(" Column I ",,,"Column II"),("(A) The net charge crossing the 4 volt cell in "mu"C is",,,"(p) 2"),("(B) The magnitude of work done by 4 Volt cell in " mu "J is",,,"(q) 6"),("(C) The gain in potential energy of capacitor in " mu "J is ",,,"(r) 8"),("(D) The net heat produced in circuit in " mu"J is ",,,"(s) 16"):}
A solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(bgt a ). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as V_b . After taking these readings, he decides . to put charge of -4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is /_\V . He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q_2 . He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q_3 . Potential difference (/_\CV) measured by the student between the inner solid shere and outer shell after putting a charge -4Q is
A solid conducting sphere of radius 10 cm is enclosed by a thin metallic shell of radius 20 cm . A charge q = 20 mu C is given to the inner sphere is connected to the shell by a conducting wire.
Assertion : When two charged spheres are connected to each other by a thin conducting wire, charge flow bigger sphere to smaller sphere, if initial charges on them are same. Reason : Electrostatic potential energy will be lost in redistribution of charges.
Figure shows two conducting spheres separated by large distance and of radius 2 cm and 3 cm containing charges 10 muC and 20 muC respectively. When the spheres are connected by a conducting wire then find out following : (i) Ratio of the final charge. (ii) Final charge on each sphere. (iii) Ratio of final charge densities. (iv) Heat produced during the process.
Three concentric conducting spherical shells of radii R, 2R and 3R carry charges Q, - 2Q and 3Q , respectively. a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre . b. Compute the electric field at r=5/2R c. Compute the total electrostatic energy stored in the system. The inner shell is now connected to the external one by a conducting wire, passing through a very small hole in the middle shell. d. Compute the charges on the spheres of radii R and 3R . e. Compute the electric field at r=5/2R
Figure shows two conducting thin concentric shells of radii r and 3 r . The outer shell carries charge q and the inner shell is neutral . The amount of charge that flows from the inner shell to the earth after the key K is closed is equal to (1//n)^(th) of the charge on the outer shell. What is the value of n ? .
A metal sphere of radius 'a' is having charge +Q . Now it is connected by a conducting wire concentric spherical shell of radius '2a'. Then the potential at the surface of outer shell is Here, K=(1)/(4pi epsilon_(0))