Home
Class 12
PHYSICS
A boy standing at the top of a tower of ...

A boy standing at the top of a tower of 20 m height drops a stone. Assuming `g = 10 ms ^-2),` the velocity with which it hits the ground is

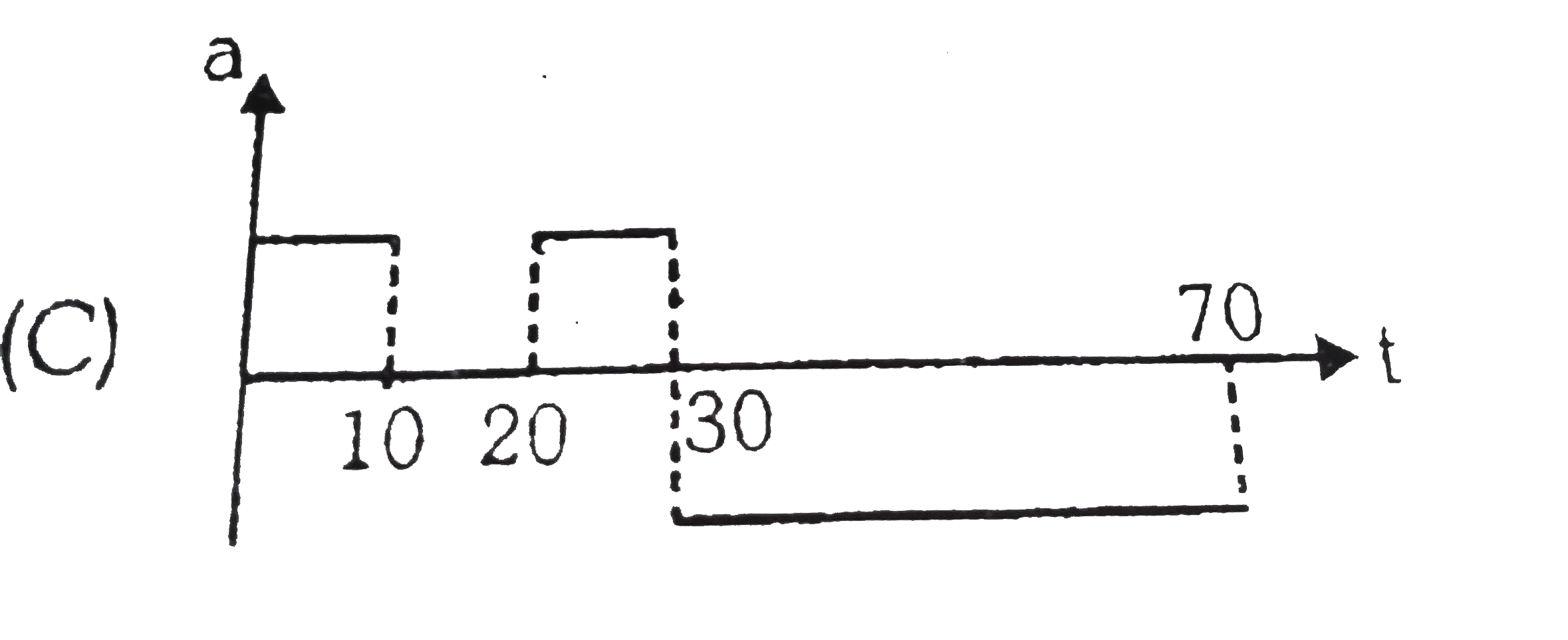
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
D
Positive slopes have positive acceleration, negative slopes have negative acceleration.
Promotional Banner

Topper's Solved these Questions

  • MOTION IN A PALNE

    ALLEN|Exercise Comprehension#3|5 Videos

  • MOTION IN A PALNE

    ALLEN|Exercise Comprehension#4|3 Videos

  • MOTION IN A PALNE

    ALLEN|Exercise Comprehension#1|3 Videos

  • KINEMATICS-2D

    ALLEN|Exercise Exercise (O-2)|46 Videos

  • NEWTON'S LAWS OF MOTION & FRICTION

    ALLEN|Exercise EXERCISE (JA)|4 Videos

Similar Questions

Explore conceptually related problems

A boy standing at the top of a tower of 20m of height drops a stone. Assuming g=10ms^(-2) , the velocity with which it hits the ground is :-

A boy standing at the top of a tower of 20 m . Height drops a stone. Assuming g = 10 ms^-2 towards north. The average acceleration of the body is.

A stone is thrown horizontally with velocity g ms^(-1) from the top of a tower of height g metre. The velocity with which it hits the ground is (in ms^(-1) )

A body is dropped freely under gravity from the top of a tower of height 78.4 m. Calculate : the velocity with which it strikes the ground. Take g = 9.8 m s^(-2) .

A ball is dropped from a height of 20 m and rebounds with a velocity which is 3/4 of the velocity with which it hits the ground. What is the time interval between the first and second bunces (g=10m//s^(2))

A boy standing on the top of a tower of height 54 ft. throws a packet with a speed of 20 ft/s directly aiming towards his friend standing on the ground at a distance of 72 ft from the foot of the tower. The packet falls short of the person on the ground by x xx(16)/(3) ft. The value of x is

A stone is thrown horizontally with the velocity u = 15m/s from a tower of height H = 25 m. Find (i) the time during which the stone is in motion , (ii) the distance from the tower base to the point where the stone will touch the ground (iii) the velocity v with which it will touch the ground (iv) the angle theta the trajectory of the stone makes with the horizontal at the point stone touches the ground (Air resistance is to be neglected). (g=10ms^(-2)) .

A stone is thrown vertically up at 20 m/s from a tower 80 m height. The speed with which it hits the ground is [g=10 "m/s"^2]

A stone is dropped freely from the top of a tower and it reaches the ground in 4 s. Taking g = 10 m s^(-2) , calculate the height of the tower.

A stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100 ms^(-1) . Find when and where the two stones meet ?