The area under velocity-time graph gives the displacement whereas the slope of velocity-time graph at any point gives acceleration at that point. Slope is +ve if the line makes an acute angle in the anticlockwise direction with respect to the positive direction along which the independent variable increases. From the calculus, we also know that the slope of the tangent to a y vs. x graph is given by `(dy)/(dx)` If `(dy)/(dx)` is +ve then y increases with x, otherwise it decreases. Consider two persons namely Ram, and Rahim, who have gone to picnic at a nice place. Finding a beautiful place they rush towards it simultaneously. Let us take the time when they start simultaneously at t= 0 and at this instant the position of Ram and Rahim be x = 0 and x = + 48, respectively. Ram maintains a uniform velocity of +10 m/s throughout the journey whereas Rahim starts from rest and continuously accelerates with + `1 m//s^(2)`
Q The position-time graph for the motions of Ram and Rahim is given by

Options

A.
B.
C.
D.

Answer

To solve the problem, we need to analyze the motion of two individuals, Ram and Rahim, based on the information provided.

### Step-by-Step Solution:

1. **Understand the Initial Conditions**:
- Ram starts at position \( x = 0 \) and moves with a uniform velocity of \( +10 \, \text{m/s} \).
- Rahim starts at position \( x = +48 \) and starts from rest, accelerating at \( +1 \, \text{m/s}^2 \).

2. **Determine the Position Function for Ram**:
- Since Ram moves with a constant velocity, the position \( x_R \) as a function of time \( t \) can be expressed as:
\[ x_R(t) = 10t \]

3. **Determine the Position Function for Rahim**:
- Rahim starts from rest and accelerates. The position \( x_H \) as a function of time \( t \) can be expressed using the equation of motion:
\[ x_H(t) = x_0 + v_0 t + \frac{1}{2} a t^2 \]
- Here, \( x_0 = 48 \), \( v_0 = 0 \), and \( a = 1 \, \text{m/s}^2 \). Thus, the equation becomes:
\[ x_H(t) = 48 + 0 \cdot t + \frac{1}{2} (1) t^2 = 48 + \frac{1}{2} t^2 \]

4. **Combine the Position Functions**:
- We have the position functions for both Ram and Rahim:
- Ram: \( x_R(t) = 10t \)
- Rahim: \( x_H(t) = 48 + \frac{1}{2} t^2 \)

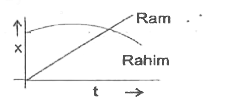
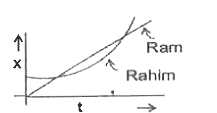
5. **Graphical Representation**:
- For Ram, the graph will be a straight line starting from the origin (0,0) with a slope of 10.
- For Rahim, the graph will start from the point (0, 48) and will be a parabolic curve opening upwards due to the acceleration.

6. **Identifying the Correct Graph**:
- The graph of Ram will be a straight line with a constant slope of 10.
- The graph of Rahim will be a curve starting from (0, 48) and will be concave upwards.
- Based on the descriptions provided, we can eliminate options that do not match these characteristics.

### Conclusion:
After analyzing the position functions and their graphical representations, the correct graph that represents the motion of Ram and Rahim is option **D**.