Consider an electric dipole AB consisting of two charges -q and +q. Let P be the point where we have to calculate the electric potential and O be the centre of dipole.
Let `OP=r`, `/_BOP=theta` and `AB=2a`.
Let `BP=r_(1)` and `AP=r_(2)`.
The potential at point P due to `+q` charge is given by
`V_(1)=(1)/(4piepsilon_(0))(q)/(r_(1))`.........(i)
The potential at point P due to -q charge is given by
`V_(2)=(1)/(4piepsilon_(0))((-q))/(r_(2))`
or `V_(2)=-(1)/(4piepsilon_(0))(q)/(r_(2))`...........(ii)
According to superposition principle the net potential at point P is given by
`V=V_(1)+V_(2)`
or `V=(1)/(4piepsioln_(0))(q)/(r_(1))-(1)/(4piepsilon_(0))(q)/(r_(2))` [using equations (i) and (ii)]
or `V=(q)/(4piepsilon_(0))[(1)/(r_(1))-(1)/(r_(2))]`............(iii)
Now draw AC perpendicular to extended segment of PO and BD perpendicular to PO as shown in the figure.
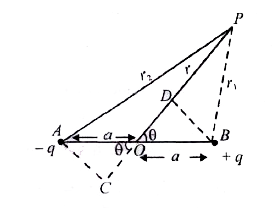
In `DeltaAOC`, `costheta=(OC)/(OA)impliesOC=OA costheta=a costheta`
In `DeltaBOD`, `costheta=(OD)/(OB)impliesOD=OBcostheta=acostheta`
Now `r_(1)=BP~~PD=OP-OD=r-acostheta`...........(iv)
`r_(2)=AP~~CP=OP+OC=r+acostheta` .................(v)
Using equations (iv) and (v) , equation (iii) becomes
`V=(q)/(4piepsilon_(0))[(1)/(r-acostheta)-(1)/(r+acostheta)]=(q)/(4piepsilon_(0))[(r+acostheta-r+acostheta)/(r^(2)-a^(2)cos^(2)theta)]`
or ` V=(q)/(4piepsilon_(0))[(2acostheta)/(r^(2)-a^(2)cos^(2)theta)]=(1)/(4piepsilon_(0))[((qxx2a)costheta)/(r^(2)-a^(2)cos^(2)theta)]`
or `V=(1)/(4piepsilon_(0))[(pcostheta)/(r^(2)-a^(2)cos^(2)theta)]` `[ :.p=qxx2a]`..........(vi)
(i) Axial Line : When point P is on axial line , then `theta=0^(@)`.
So equation (vi) becomes
`V_(a)=(1)/(4piepsilon_(0))=(pcostheta)/((r^(2)-a^(2)cos^(2)theta))=(1)/(4piepsilon_(0))(p)/((r^(2)-a^(2)))`
(ii) Equatorial Line : When point P is on equatorial line, then `theta=90^(@)`, so equation (vi) becomes
`V_(eq)=(1)/(4piepsilon_(0))(pcos90^(@))/((r^(2)-a^(2)cos^(2)90^(@)))=0`
So electric potential on equatorial line is zero.
