A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LINEAR PROGRAMMING
ACCURATE PUBLICATION|Exercise QUESTIONS CARRYING 1 MARK (TYPE-II : FILL IN THE BLANKS QUESTIONS) |11 VideosLINEAR PROGRAMMING
ACCURATE PUBLICATION|Exercise QUESTIONS CARRYING 1 MARK (TYPE-III : TRUE OR FALSE QUESTIONS)|10 VideosLINEAR PROGRAMMING
ACCURATE PUBLICATION|Exercise QUESTIONS CARRYING 6 MARKS |7 VideosINVERSE TRIGONOMETRIC FUNCTIONS
ACCURATE PUBLICATION|Exercise QUESTIONS CARRYING 4 MARKS|27 VideosMATRICES
ACCURATE PUBLICATION|Exercise QUESTIONS CARRYING 6 MARKS |4 Videos
Similar Questions
Explore conceptually related problems
ACCURATE PUBLICATION-LINEAR PROGRAMMING -QUESTIONS CARRYING 1 MARK (TYPE-I : MULTIPLE CHOICE QUESTIONS)
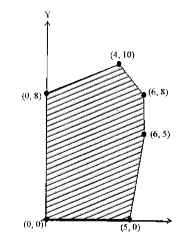
- The feasible solution for a LPP is shown in Fig. Let. Z = 3x - 4 y be ...
Text Solution
|
- The feasible solution for a LPP is shown in Fig. Let. Z = 3x-4 y be th...
Text Solution
|
- The feasible region for an LPP is shown in the figure. Let F = 3 x - 4...
Text Solution
|
- The feasible solution for a LPP is shown in Fig. Let. Z = 3x-4 y be th...
Text Solution
|
- Corner points of the feasible region for an LPP are (0,2), (3,0), (6,0...
Text Solution
|
- Corner points of the feasible region determined by the system of linea...
Text Solution
|
- The corner points of the feasible region determined by the system of l...
Text Solution
|
- The point which does not lie in the half-plane 3x+7 y-32 le 0 is
Text Solution
|
- Quadrant represented by the region xge0, y le0 is
Text Solution
|
- The corner points of the feasible region determined by the system of l...
Text Solution
|
- The feasible solution for a LPP is shown in Fig. Let, Z=3x-4 y be the ...
Text Solution
|
- The feasible region for an LPP is shown in the figure . Let F = 3 x - ...
Text Solution
|
- Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6...
Text Solution
|
- The point which does not lie in the half-plane 4x+5 y-36 le 0 is
Text Solution
|
- Quadrant represented by the region x ge 0, y ge 0 is first.
Text Solution
|