Point masses m1 and m2 are placed at th...

Point masses` m_1` and `m_2` are placed at the opposite ends of a rigid rod of length L, and negligible mass . The position of point p on this rod through which the axis should p on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity `omega_0` is minimum , is given by:
.

`x=m_2L/(m_1+m_2)`

`x=m_1L/(m_1+m_2)`

`x=(m_1)/(m_2)L

`x=(m_2)/(m_1)L`

Text Solution

Verified by Experts

Topper's Solved these Questions

GRAVITATION
SARAS PUBLICATION|Exercise EXAMPLE|34 Videos
LAWS OF MOTION
SARAS PUBLICATION|Exercise EXAMPLE|16 Videos

Similar Questions

Explore conceptually related problems

A rod of length L and mass M is hinged at point O. A small bullet of mass m ihits the rod with velocity v as shown in the figure. The bullet gets embedded in the rod. Calculate the angular velocity of the system just after the impact?

Three mass points m_(1)m_(2) amd m_(3) are located at the vertices of an equilateral triangle of length a. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m_(1) ?

Two particles of masses m_1 and m_2 are joined by a light rigid rod of length r. The system rotates at an angular speed omega about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is L=mur^2omega where mu is the reduced mass of the system defined as mu=(m_1m_2)/(m_1+m_2)

A unifrom rod AB of length l,and mass m is free to rotate about point A.The rod is release from rest in the horizontal position Given that the moment of inertia of the rod about A is (ml^2)/3 , the initial angular acceleration of the rod will be:

A rod of length 1.2 m moves with its ends always touching the coordinate axes. The locus of a point Pon the rod, which is 0.3 m from the end in contact with x-axis is an ellipse. Find the eccentricity.

Moment of inertia of a thin uniform rod about an axis passing through the center of mass and perpendicular to the length is

SARAS PUBLICATION-KINEMATICS-EXAMPLE

The distance travelled by a particle starting from rest and moving wit...
Text Solution
|
A thin circular ring of mass M and radius R is rotating in a horizonta...
Text Solution
|
A rectangular, a square, a circular and an elliptica loop, all in the ...
Text Solution
|
Six vectors , a through f have the magnitude and directions indicat...
Text Solution
|
The dimensions of (mu0 epsilon0)^(-1/2) are :
Text Solution
|
The instantaneous angular position of a point on a rotating wheel is g...
Text Solution
|
Two spheres A and B of masses m1 and m2 respectively collide . A is at...
Text Solution
|
The velocity of a projectile at the initial point A is (2 hati +3 hatj...
Text Solution
|
A stone falls freely under gravity . It covers distances h1 h2 and h3 ...
Text Solution
|
A small object of uniform density rolls up a curved surface with an in...
Text Solution
|
Vectors vecA, vecB and vec C are such that vecA.vecB =0 and vecA. vecC...
Text Solution
|
The displacement ‘x’ (in meter)of a particle of mass ‘m’ (in kg) mo...
Text Solution
|
A particle is moving such that its position coordinates (x,y) are (2m,...
Text Solution
|
A balloon with mass m is descending down with an acceleration a (where...
Text Solution
|
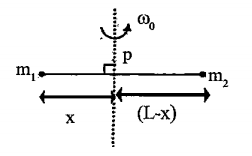
Point masses m1 and m2 are placed at the opposite ends of a rigid ro...
Text Solution
|
What is the minimum velocity with a body of mass m must enter a vertic...
Text Solution
|
If the magnitude of sum of two vectors is equal to the magnitude of di...
Text Solution
|
Two cars P and Q starts from a point at the same time in a straight li...
Text Solution
|
Preeti reached the metro station and found that the escalator was not ...
Text Solution
|
The x and y coordination of the particle at any time are x=5t - 2t^2an...
Text Solution
|