Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CIRCLES
SWAN PUBLICATION|Exercise Exercise 10.1 (Fill in the blanks)|4 VideosView PlaylistARITHMETIC PROGRESSIONS
SWAN PUBLICATION|Exercise Exercise 5.4|5 VideosView PlaylistCONSTRUCTIONS
SWAN PUBLICATION|Exercise EXERCISE 11.2|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
SWAN PUBLICATION-CIRCLES-Exercise 10.2
- From a point Q, the length of the tangent to a circle is 24 cm and the...
01:58
|
Play - In Fig., if TP and TQ and two tangents to a circle with centre O so th...
01:33
|
Play - If tangents PA and PB from a point P to a circle with centre O are inc...
02:07
|
Play - Prove that the tangents drawn at the ends of a diameter of a circle ar...
02:34
|
Play - Prove that the perpendicular at the point of contact to the tangent to...
05:53
|
Play - The length of a tangent from a point A at distance 5 cm from the centr...
04:40
|
Play - Two concentric circles are of radii 5 cm and 3 cm. Find the length of ...
06:52
|
Play - A quadrilateral ABCD is drawn to circumscribe a circle(seeFig).Prove t...
05:01
|
Play - Prove that the angle between the two tangents drawn from an external p...
01:55
|
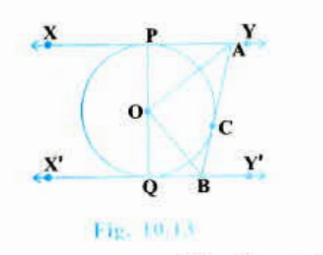
Play - In Fig, 10.13, XY and X'Y' are two parallel tangents to a circle with ...
08:32
|
Playing Now - Prove that the parallelogram circumscribing a circle is a rhombus.
04:38
|
Play - A triangle ABC is drawn to circumscribe a circle of radius 4 cm such t...
15:28
|
Play - Prove that opposite sides of a quadrilateral circumscribing a circle s...
10:43
|
Play