Home
Class 6
MATHS
You have two set -squares in your mathem...

You have two set -squares in your mathematical instruments box . Are they symmetric ?
There are two set squares in our mathematical instruments box , they are :
(i) `30^(@) - 60^(@) - 90^(@)` set square

(ii) `45^(@)- 45^(@)-90^(@)` set square

Answer

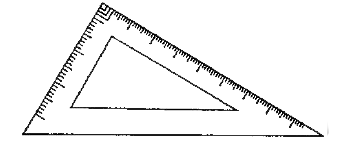
Step by step text solution for You have two set -squares in your mathematical instruments box . Are they symmetric ? There are two set squares in our mathematical instruments box , they are : (i) 30^(@) - 60^(@) - 90^(@) set square (ii) 45^(@)- 45^(@)-90^(@) set square by MATHS experts to help you in doubts & scoring excellent marks in Class 6 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • SYMMETRY

    NAND LAL PUBLICATION|Exercise Exercise - 13.1 |7 Videos

  • SYMMETRY

    NAND LAL PUBLICATION|Exercise Exercise -13.2 |11 Videos

  • SYMMETRY

    NAND LAL PUBLICATION|Exercise Do this |7 Videos

  • RATIO AND PROPORTION

    NAND LAL PUBLICATION|Exercise SAMPLE PAPER FOR PRACTICE |13 Videos

  • UNDERSTANDING ELEMENTARY SHAPES

    NAND LAL PUBLICATION|Exercise SAMPLE PAPER FOR PRACTICE (Fill in the blanks)|6 Videos

Similar Questions

Explore conceptually related problems

45^(@) -90^(@) - 45^(@) set square does not exist

The number of lines of symmetry in 30^(@) -60^(@)-90^(@) set square is

There are two" set-square" in your box.What are the measures of the anles that ae formed at their corners?Do they have any angle measure that is common?

In a pair of set-squares the order is with angles :

Using two set squares angle of 75^(@) can be drawn

Ruler and a pair of set square can be used to draw

One of the two set squares in your instrument box has angles of measure 30^(@) - 60^(@) - 90^(@) Take two such identical set - squares .Place them side by side to form a kite like the one shown here . How many lines of symmetry does the shape have ? Do you think that some shapes may have more than one line of symmetry ?

Shade (i) 1/2 of circles in box (a) (ii) 2/3 of the triangles in box (b) (iii) (3)/(5) of the squares in box (c )

Whether the following statement is true ? Justify your answer. The set of all rectangles is contained in the set of squares.

A square matrix A with elements form the set of real numbers is said to be orthogonal if A' = A^(-1). If A is an orthogonal matris, then

Home
Profile