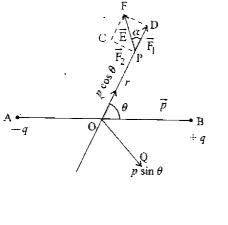
Recommended Questions
- Derive an expression for electric field intensity at any point due to ...
Text Solution
|
Playing Now - Electric Field Intensity Due To A Short Dipole At Some General Point
08:03
|
Play - Derive an expression for the intensity of the electric field at a poin...
07:05
|
Play - Derive an expression for the intensity of the electric field at a poin...
08:59
|
Play - Derive an expression for the electric field due to an electric dipole ...
10:33
|
Play - Derive an expression for electric field due to an electric dipole at a...
10:33
|
Play - Define electric field intensity at a point. Give its S.I. units. Deriv...
07:01
|
Play - Derive an expression for electric field due to an electric dipole at a...
10:33
|
Play - Derive an expression for electric field intensity at a point on the ax...
05:34
|
Play