Home
Class 12
PHYSICS
Derive electric field intensity due to u...

Derive electric field intensity due to uniformity charged infinite plane sheet

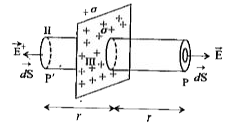
Text Solution

Verified by Experts

Consider a thin infinite plane sheet.
Let P = be a point where we want to find electric field intensity `vec(E)`.
`sigma =` be the surface charge density.
`i.e.," "sigma=q/A` `:." "`the charge enclosed by Gaussian surface,
`q=sigmaA`
According to Gauss is theorem
`underset(S)ointvecE.vec(dS)=q/varepsilon_(0)=(sigmaA)/varepsilon_(0)`
Gaussian surface is divided into three parts I, II and III.
`:." "`From (1)
`underset(I)ointvecE.vec(dS)+underset(II)ointvecE.vec(dS)+underset(III)ointvecE.vec(dS)=(sigmaA)/varepsilon_(0)" "...(2)`
`underset(I)ointEpScos theta+underset(II)ointEpScos theta+underset(III)ointEpScos theta = (sigma A)/varepsilon_(0)`
`underset(I)ointEpScos 0^(@)+underset(II)ointEpScos 0^(@)+underset(III)ointEpScos 90^(@) = (sigma A)/varepsilon_(0)`
`underset(I)ointEpS+underset(II)ointEpS+0 = (sigma A)/varepsilon_(0)`
`underset(I)ointEpS(1)+underset(II)ointEpS(1) = (sigma A)/varepsilon_(0)`
`underset(I)ointEpS+underset(II)ointEpS = (sigma A)/varepsilon_(0)`
Since electric field intensity E is constant at every point of Gaussian surface,
`:." "Eunderset(I)ointds+Eunderset(II)ointds=(sigmaA)/varepsilon_(0)`
`EA+EA=(sigmaA)/varepsilon_(0)`
`2EA=(sigmaA)/varepsilon_(0)`
`EA=(sigmaA)/(2varepsilon_(0))`
`:." "E=(sigmaA)/(2varepsilon_(0)A)`
`:." "E=sigma/(2 varepsilon_(0))`
`:." "`In vector from
`vecE=sigma/(2varepsilon_(0))hatn`, where `hatn` is a unit vector perpendiculars to the plane of sheet.
The electric field is directed away from the sheet if it is positively, charged and it is directed towards the sheet if it is negatively charged.
Special Case
If the plane sheet has a finite thickness, then charges on both sides of sheet are to be considered.
`:." "E=(2 sigmaA)/(2varepsilon_(0)A)`
`:." "E=sigma/varepsilon_(0)`
Doubtnut Promotions Banner Mobile Dark
|

Similar Questions

Explore conceptually related problems

State and prove Gauss's theorem of electrostatic. Derive an expression for the electric field intensity due to uniformly charged infinite plane sheet.

What is electric flux? Write its SI units. Using Gauss. Theorem, derive an expression for electric theorem, derive an expression for electric field at a point due to uniformaly charged infinite plane sheet.

Using Gauss's theorem derive an expression for electric field intensity at a point due to an infinite plane sheet of charge. Or What is Gauss's law in electrostatics? Using it, obtain an expression for electric field due to uniformly charged thin infinite plane sheet. What would happen, if sheet is thick?

Derive electric field intensity due to uniformly charged ring or circular loop.

State Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point outside

State Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point inside

State Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point on the surface of the spherical shell.

State Gauss' law and using this law , derive an expression for the electric field intensity due to a uniformly charged thin spherical shell at a point inside

State Gauss' law and using this law , derive an expression for the electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell.

Using Gauss's Theorem, Derive an expression for electric field intensity due to uniformity charged hollow sphere : (b) At a point on the shell

Home
Profile