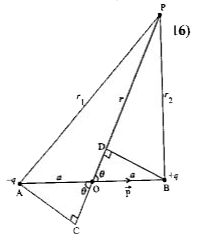
Let P = be any point at a distance r from O.
`r_(1)=AP`
`r_(2)=BP`
`theta=` be the angle between OP and dipole moment `vecp` .
Consider an electric dipole AB having charge (-q) at point A and charge (+q) at point B. Let O be the centre to the dipole.
The electric potential at P due to -q charge is given by
`V_(1)=1/(4 pi varepsilon_(0))((-q))/r_(1)`
`V_(1)=1/(4 pi varepsilon_(0))(q)/r_(1)" "...(1)`
`:." "`Potential at P due to + charge is given by
`V_(1)=1/(4 pi varepsilon_(0))q/r_(2)" "...(2)`
Using principle of superposition,
`V=V_(1)+V_(2)`
`:." "V=(-1)/(4 pi varepsilon_(0))q/r_(1)+1/(4 pi varepsilon_(0))`
`:." "V=q/(4 pi varepsilon_(0))[1/r^(2)-1/r_(1)]" "...(3)`
Draw a perpendicular from A which meets the line OP at C when produced such that `AP~~PC`. Also draw the BD perpendicular on OP such that `BP~~PD`.
Now, In `Delta OAC`.
`cos theta=(OC)/(OA)`
`costheta=(OC)/a`
`OC=a cos theta`
In `Delta OBD," "cos theta=(OD)/(OB)`
`cos theta=(OD)/a implies OD = a cos theta`
Then `r_(1)=OP+OC=r+a cos theta`
`r_(2)=OP-OD=r-a cos theta`
Substituting the values in equation (3)
`:." "V=q/(4 pi varepsilon_(0))[1/((r-a cos theta))-1/((r+a cos theta))]`
`V=q/(4 pi varepsilon_(0))[(r+a cos theta-(r-a cos theta))/(r^(2)-a^(2)cos^(2)theta)]`
`V=q/(4 pi varepsilon_(0))[(r+a cos theta-r+a cos theta)/(r^(2)-a^(2)cos^(2)theta)]`
`V=q/(4 pi varepsilon_(0))[(2a cos theta)/(r^(2)-a^(2) cos^(2)theta)]`
Since, `(q xx 2a=p)`
`V=(q xx 2 a cos theta)/(4 pi varepsilon_(0)[r^(2)-a^(2)cos^(2)theta])`
`:." "V=(p cos theta)/(4 pi varepsilon_(0)(r^(2)-a^(2)cos^(2)theta))`
when r>>>>a, then `a^(2)` can be neglected in comparison to `r^(2)`.
`:." "V = (p cos theta)/(4 pi varepsilon_(0)r^(2))`
(i) When point P lies on the axial line
then`" "thrta=0^(@)`
`:." "V=(p cos0^(@))/(4 pi varepsilon_(0)r^(2))`
`V=p/(4 pi varepsilon_(0)r^(2))`
`i.e.," "V prop 1/r^(2)`
(2) If point P lies on the equatorial line of dipole
then`" "theta = 90^@`
`V = (p cos 90^@)/4 pi varepsilon_(0)r^(2))`
`V=0" "[:. cos 90^(@)=0]`
`:." "`Electric potential due to dipole is zero on all points on equatorial line.