Answer
Step by step text solution for DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig. ).If AD is extended to intersect BC at P, show that DeltaABD ~= DeltaACD. by MATHS experts to help you in doubts & scoring excellent marks in Class 9 exams.
|
Topper's Solved these Questions
TRIANGLES
SWAN PUBLICATION|Exercise EXERCISE 7.4|6 VideosView PlaylistTRIANGLES
SWAN PUBLICATION|Exercise EXERCISE 7.5|4 VideosView PlaylistTRIANGLES
SWAN PUBLICATION|Exercise EXERCISE 7.2|10 VideosView PlaylistSURFACE AREAS AND VOLUMES
SWAN PUBLICATION|Exercise Objective Type Questions (Fill in the Blanks ) |7 VideosView Playlist
Similar Questions
Explore conceptually related problems
SWAN PUBLICATION-TRIANGLES -EXERCISE 7.3
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
03:17
|
Playing Now - DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
03:17
|
Play - DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
08:09
|
Play - DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
03:17
|
Play - AD is an altitude of an isosceles triangle ABC in which AB = AC. Show ...
07:19
|
Play - AD is an altitude of an isosceles triangle ABC in which AB = AC. Show ...
07:19
|
Play - Two sides AB and BC and median AM of one triangle ABC are respectively...
05:05
|
Play - Two sides AB and BC and median AM of one triangle ABC are respectively...
05:05
|
Play - BE and CF are two equal altitudes of a triangle ABC. Using RHS congrue...
04:25
|
Play - ABC is an isosceles triangle with AC = BC. If AB^2 = 2AC^2, prove that...
02:19
|
Play
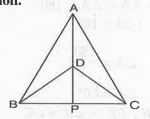 ).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.
).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.