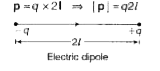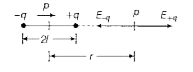Electric Dipole Two point charges of same magnitude and opposite nature separated by a small distance from each other form an electric dipole .
Electric Dipole Moment The strength of an electric dipole is measured by a vector quantity known as electric dipole moment . `vecp` . it is the product of the charge q and separation between the charges 2l.
p = `q xx 2l implies |p| = q 2 l `
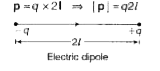
Direction Its direction is from negative charge `-q` to positive charge +q .
The SI unit of electric dipole moment is coulomb - metre and it is denoted by symbol p .
(i) Electric Field Intensity at any Point on the Axial Line/End on Position of Electric Dipole
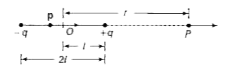
As shown in the figure consider an electric dipole consisting of charges +q and -q , separated by a distance 2 l and placed in separated by a distance 2l and placed in vacuum . Let P be a point on the axial line at distance r from the centre O of the dipole on the side of the charge +q .
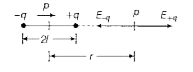
Electric field due to charge -q at point P is `E_(-q) = (-q)/(4 pi epsi_(0) ( r + l)^(2)) hatp` (towards left)
where `hatp` is a unit vector along the dipole axis from -q to +q .
Electric field due to charge `+q` at point P is `E_(+q) = (q)/(4 pi epsi_(0) (r - l)^(2)) hatp` (towards right)
Hence , the resultant electric field at the point P is `E_("axial") = E_(+q) + E_(-q)`
`= (q)/(4pi epsi_(0)) [ (1)/(( r- l)^(2)) - (1)/((r + l)^(2))] hatp`
`= (q)/(4pi epsi_(0)) * (4 lr)/((r^(2) - l^(2))^(2)) hatp`
or `E_("axial") = (1)/(4 pi epsi_(0)) * (2p r)/((r^(2) -l^(2))^(2)) hatp`
Here p = ` q xx 2 l` = dipole moment
When `l lt lt r`
`E_("axial") = (1)/(4 pi epsi_(0)) * (2p)/(r^(3))`
`implies |E_("axial")| = (1)/(4 pi epsi_(0)) * (2 |p|)/(r^3)`
`E prop (1)/(r^3)`

The direction of the electric field at any point on axial line is along the direction of electric dipole moment .