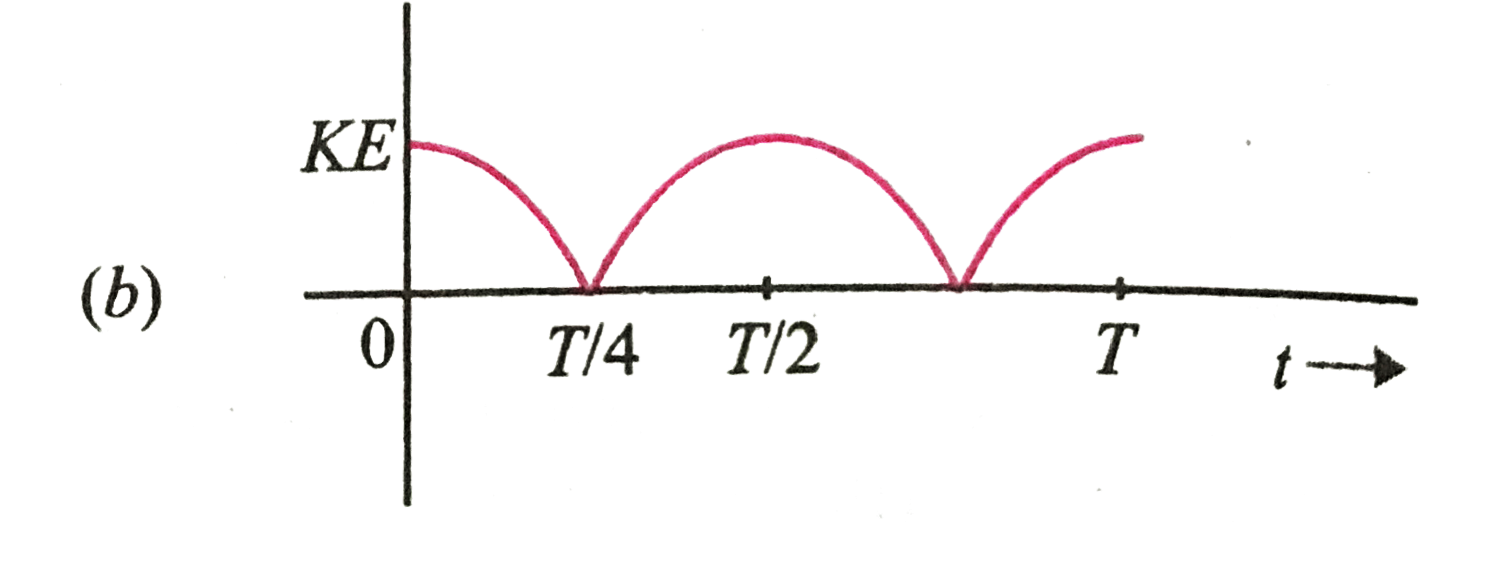
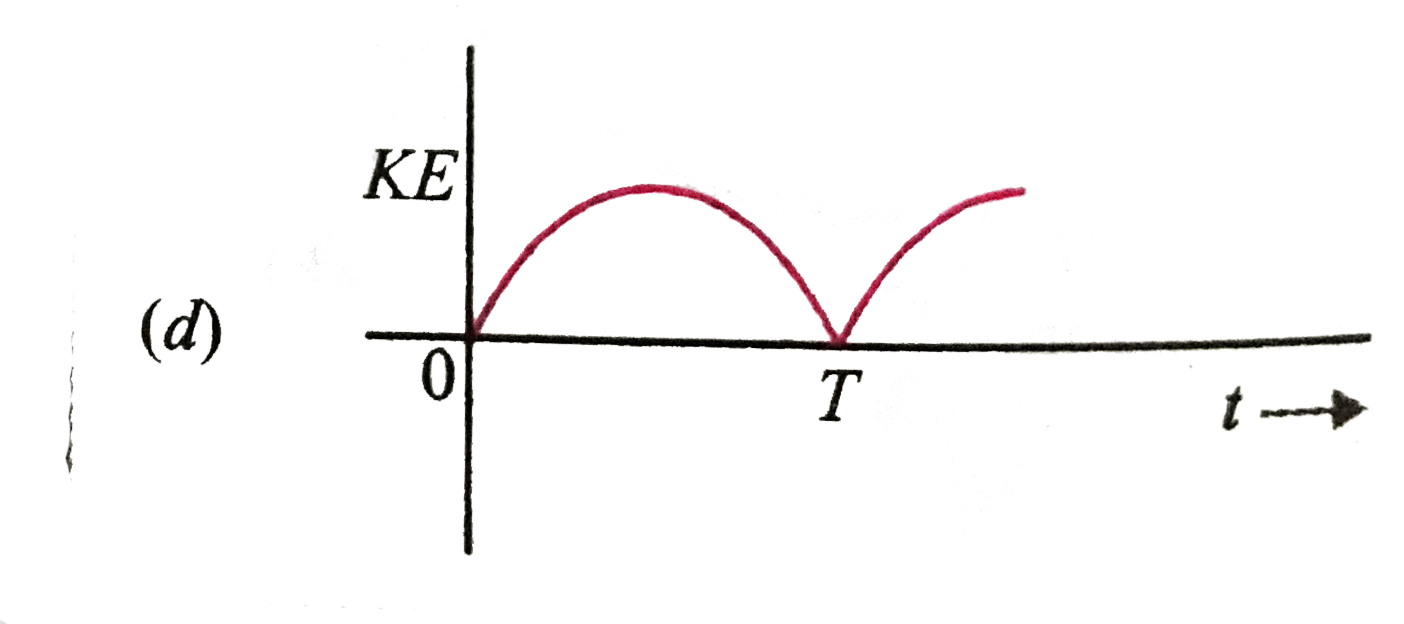
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
JEE MAIN 2021
JEE MAINS PREVIOUS YEAR|Exercise PHYSICS SECTION B|30 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
JEE MAINS PREVIOUS YEAR-JEE MAIN-All Questions
- A particle of mass 1 kg is hanging from a spring of force constant 100...
01:41
|
Playing Now - If weight of an object at pole is 196 N then weight at equator is [g =...
05:16
|
Play - In a house 15 Bulbs of 45 W, 15 bulbs of 100 W, 15 bulbs of 10 W and T...
03:15
|
Play - In an adiabatic process, volume is doubled then find the ratio of fina...
04:52
|
Play - A block of mass 10kg is suspended from string of length 4m. When pulle...
01:41
|
Play - The surface mass density of a disc of radius a varies with radial dist...
06:45
|
Play - Cascaded Carnot engine is an arrangement in which heat sink of one eng...
04:24
|
Play - Activity of a substance changes from 700 s^(–1) to 500 s^(–1) in 30 mi...
02:39
|
Play - In YDSE, separation between slits is 0.15 mm, distance between slits a...
02:18
|
Play - An ideal fluid is flowing in a pipe in streamline flow. Pipe has maxim...
04:18
|
Play - There is a electric circuit as shown in the figure. Find potential dif...
04:32
|
Play - A particle of mass m and positive charge q is projected with a speed o...
03:52
|
Play - Two sources of sound moving with same speed v and emitting frequency o...
02:35
|
Play - An electron & a photon have same energy E. Find the ratio of de Brogli...
02:47
|
Play - A ring is rotated about diametric axis in a uniform magnetic field per...
06:03
|
Play - Electric field in space is given by vec(E(t)) = E0 (i+j)/sqrt2 cos(ome...
06:04
|
Play - Focal length of convex lens in air is 16 cm (mu(glass) = 1.5). Now the...
03:55
|
Play - A lift of mass 920 kg has a capacity of 10 persons. If average mass of...
03:16
|
Play - The hysteresis curve for a material is shown in the figure. Then for t...
02:47
|
Play - An inductor of inductance 10 mH and a resistance of 5 is connected to...
04:44
|
Play - Find the dimension of B^2/(2 mu0)
02:02
|
Play