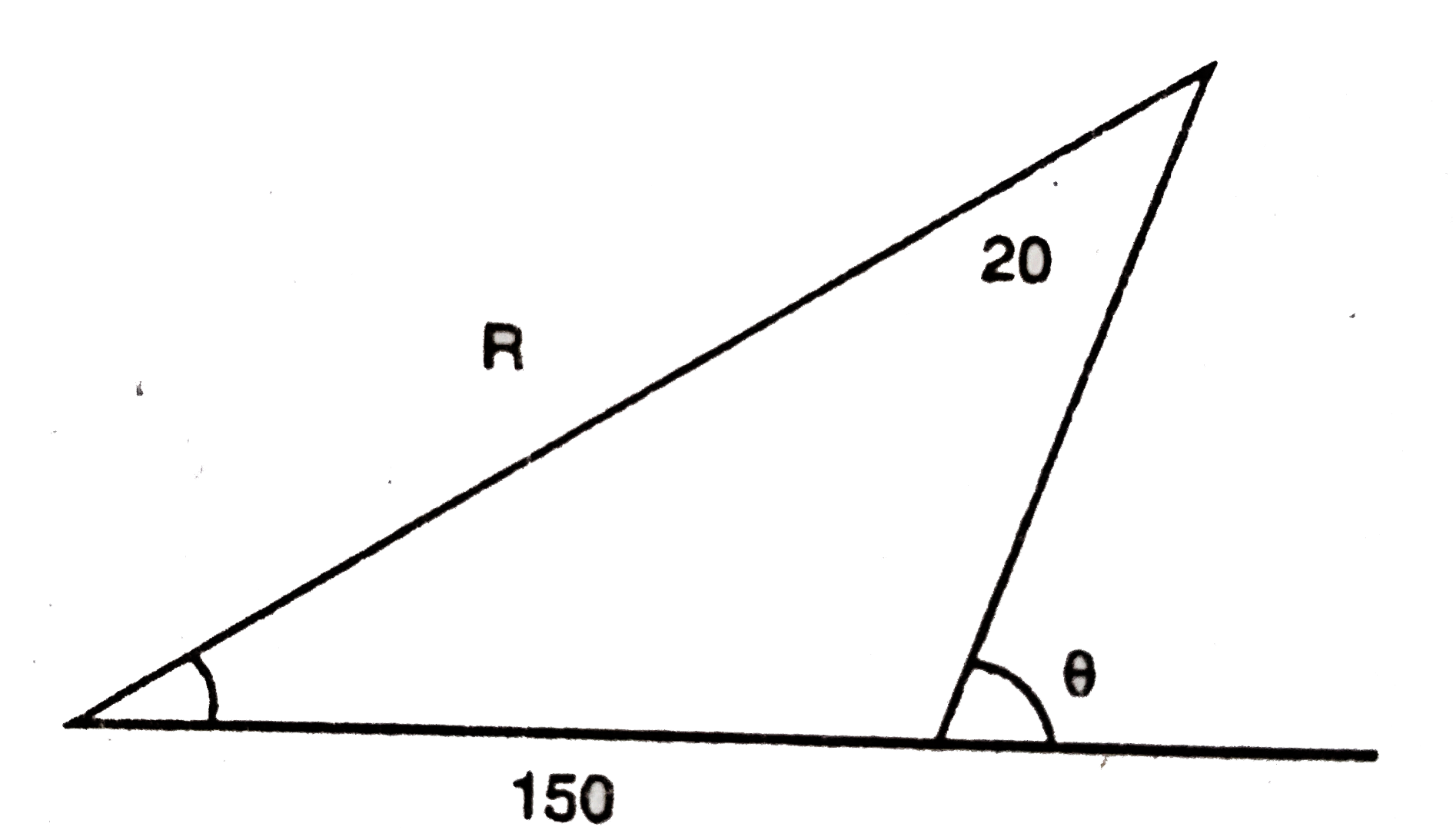
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
REST AND MOTION : KINEMATICS
HC VERMA|Exercise Objective -2|10 VideosView PlaylistPHYSICS AND MATHEMATICS
HC VERMA|Exercise Exercises|34 VideosView PlaylistROTATIONAL MECHANICS
HC VERMA|Exercise Exercises|86 VideosView Playlist
Similar Questions
Explore conceptually related problems
HC VERMA-REST AND MOTION : KINEMATICS-Exercises
- A ball is thrown at a speed of 40 m/s at an angle of 60^0 with the hor...
03:27
|
Play - A ball whose Kinetic Energy is E is projected at an angle of 45^(@) to...
02:11
|
Play - A gun is fired from a place which is at distance 1.2 km from a hill. T...
02:12
|
Play - Figure shows a 11.7 ft wide ditch with the approach roads at and angle...
03:50
|
Play - A person standing on the top of a cliff 171 ft high has to throw a pac...
07:43
|
Play - A projectile is fired at an angle of 45 ^ { \circ } with the horizonta...
04:09
|
Play - The expression for maximum height attained when the body is projected ...
04:25
|
Play - A bomb is dropped from a plane flying horizontally with uniform speed....
04:46
|
Play - A boy standing on a long railroad car throuws a ball straight upwards....
03:28
|
Play - A staircase contains three steps each 10 cm high and 20 cm wide figure...
02:40
|
Play - A person is standing on a truck moving with a constant velocity of 14....
04:55
|
Play - The benches of a gallery in a cricket stadium are 1 m wide and 1 m hig...
05:17
|
Play - A man is sitting on the shore of a river. He is in the line of a 1.0 m...
04:42
|
Play - A 400 m wide river is flowing at a rate of 2.0 m s^-1. A boat is saili...
04:05
|
Play - A swimmer wishes to cross a 500 m river flowing at 5 km h^-1. His spe...
01:59
|
Play - A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His sp...
10:09
|
Play - An aeroplane has to go from a point A to another point B, 500 km away ...
07:09
|
Playing Now - Two friends A and B are standing a distance x apartin an open field an...
04:32
|
Play - Two friends A and B are standing a distance x apart in an open field a...
06:39
|
Play - Six particles situated at the corners of a regular hexagon of side a m...
02:43
|
Play