Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
LAWS OF THERMODYNAMICS
HC VERMA|Exercise Short Answer|14 VideosView PlaylistLAWS OF THERMODYNAMICS
HC VERMA|Exercise Objective II|5 VideosView PlaylistKINETIC THEORY OF GASES
HC VERMA|Exercise All Questions|120 VideosView PlaylistNEWTON'S LAWS OF MOTION
HC VERMA|Exercise Exercises|42 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
HC VERMA-LAWS OF THERMODYNAMICS-Exercises
- A 100 kg block is started with a speed of 2.0 m s^(-1) on a long, roug...
06:52
|
Play - calculate the change in internal energy of a gas kept in a rigid conta...
01:44
|
Play - the pressure of a gas change linearly with volume from 10kPa, 200 cc t...
02:16
|
Play - An ideal gas is taken from an initial state i to a final state f in s...
02:21
|
Play - shows three paths through which a gas can be taken from the state A to...
02:40
|
Play - when a system is taken through the process abc shown in the fig. 80 J ...
04:26
|
Play - 50 cal of heat should be supplied to take a system from the state A t...
03:43
|
Play - calculate the heat absorbed by a system in going through the cyclic pr...
02:27
|
Play - In the given figure, the value of x is
01:44
|
Play - A substance is taken through the process abc as shown in fig, if the ...
02:24
|
Play - A gas is taken along the path AB as shown in fig, if 70 cal of heat is...
03:13
|
Play - The internal energy of a gas is given by U=1.5pV. It expands from 100...
03:01
|
Play - A gas is enclosed in a cylindrical vessel fitted with a frictionless p...
04:03
|
Play - A gas is initially at a pressure of 100 kPa and its volume is 2.0 m^(3...
05:19
|
Play - Consider the cyclic process ABCA, shown in fig, performed on a sample ...
04:43
|
Play - Fig shows the variation in the internal energy U with the volume V of ...
02:03
|
Play - Find the change in the internal energy of 2 kg of water as it heated f...
05:34
|
Play - Calculate the increase in the internal energy of 10 g of water when it...
04:59
|
Play - Fig shows a cylindrical tube of volume V with adiabatic walls containi...
04:59
|
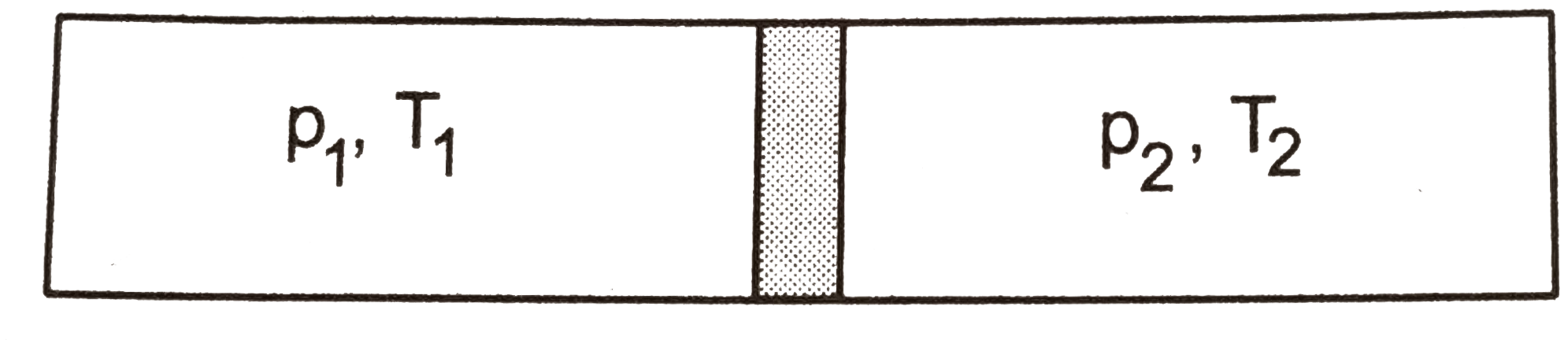
Playing Now - An adiabatic vessel of total volume V is divided into two equal parts ...
06:42
|
Play