Recommended Questions
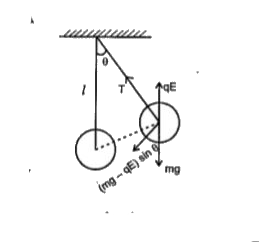
- A simple pendulum consists of a small sphere of mass m suspended by a ...
Text Solution
|
Playing Now - A simple pendulum consists of a small sphere of mass m suspended by a ...
02:12
|
Play - A simple pendulum of mass m and charge +q is suspended vertically by a...
04:16
|
Play - A Pendulum bob of mass m and charge q is suspended by a thread of leng...
Text Solution
|
Play - A simple pendulum of length I and mass (bob) m is suspended vertically...
03:08
|
Play - A simple pendulum consists of a small sphere of mass m suspended by a ...
Text Solution
|
Play - A simple pendulum has a length l and the mass of the bob is m. The bob...
03:54
|
Play - A pendulum consisting of a small sphere of mass m suspended by aninext...
02:44
|
Play - A simple pendulum consists of a small sphere of mass m suspended by a ...
Text Solution
|
Play