Home
Class 9
MATHS
In Fig ., E is any point on median ...

In Fig ., E is any point on median AD of a `DeltaABC` . Show that ar (ABE = ar (ACE) .

Answer

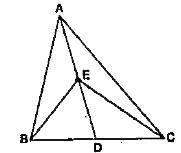
Step by step text solution for In Fig ., E is any point on median AD of a DeltaABC . Show that ar (ABE = ar (ACE) . by MATHS experts to help you in doubts & scoring excellent marks in Class 9 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • AREAS OF PARALLELOGRAMS AND TRIANGLES

    SWAN PUBLICATION|Exercise EXERCISE 9.4|21 Videos

  • AREAS OF PARALLELOGRAMS AND TRIANGLES

    SWAN PUBLICATION|Exercise OBJECTIVE TYPE QUESTIONS |20 Videos

  • AREAS OF PARALLELOGRAMS AND TRIANGLES

    SWAN PUBLICATION|Exercise EXERCISE 9.2|8 Videos

  • CIRCLES

    SWAN PUBLICATION|Exercise Objective Type Questions (Fill in the Blanks :)|10 Videos

Similar Questions

Explore conceptually related problems

E is any point on median AD of a triangle ABC . Show that ar (ABE) = ar (ACE).

E is any point on median AD of DeltaABC . If ar (DeltaABE) = 10 cm^2 then ar (DeltaACE) is :

E is any point on median AD of DeltaABC . If ar (DeltaABE) = 10 cm^2 then ar (DeltaACE) is :

In a triangle ABC , E is the mid - point of median AD . Show that ar (BED)=(1)/(4) ar (ABC).

O is any point on the diagonal PR of a parallelogram PQRS. Prove that : ar(PSO) = ar(PQO)

D and E are points on sides AB and AC respectively of DeltaABC such that ar (DBC) = ar (EBC). Prove that DE II BC .

D and E are points on sides AB and AC respectively of a DeltaABC such that ar (DeltaBCE) = ar (DeltaBCD) . Show that DE || BC .

P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).

AD is a median of DeltaABC . Is AB + BC + CA gt 2AD ?

In Fig. 7.21, AC = AE, AB = AD and angle BAD = angle EAC . Show that BC =DE.

Home
Profile