Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT TELUGU-PRACTICAL GEOMETRY -DO THIS
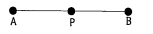
- length of bar(AP)=3cm and bar(BP)=bar(AP) in the figure. Then length o...
Text Solution
|
- Construct angles of 180^@, 240^@, 300^@.
Text Solution
|
- Construct an angle of 45^@ by using compasses.
Text Solution
|
- Express each of following decimals in the p/q form 44.162
Text Solution
|
- Construct angles of 180^@, 240^@, 300^@.
Text Solution
|
- Construct an angle of 45^@ by using compasses.
Text Solution
|