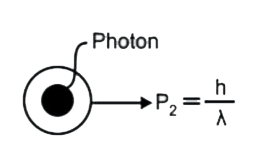
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NTA MOCK TESTS-NTA TPC JEE MAIN TEST 63-PHYSICS
- A stationary hydrogen atom emits a photon corresponding to first line ...
Text Solution
|
- In a metre bridge, the gaps are closed by two resistance P and Q and t...
Text Solution
|
- Use the output parameter to find the element type, which is the one ot...
Text Solution
|
- Given an electric field E= 2 xx 10^3 N//C is along the X – axis and p...
Text Solution
|
- (Figure 3.139) shows three circular arcs, each of radius R and total c...
Text Solution
|
- Five forces vec(F)(1) ,vec(F)(2) , vec(F)(3) , vec(F)(4) , and vec(F)(...
Text Solution
|
- A trolley of mass 20 kg is attached to a block of mass 4kg by massless...
Text Solution
|
- A U-tube closed at one end is filled with three immiscible liquids hav...
Text Solution
|
- The amplitude of damped oscillator decreased to 0.9 times its origina...
Text Solution
|
- Which of the following is equivalent to unit of inductance ?
Text Solution
|
- An aircraft of mass 4 xx 10^(5)kg with total wing area 500m^(2) in lev...
Text Solution
|
- Two blocks each of mass m lie on a smooth table. They are attached to ...
Text Solution
|
- A thin lens is made with as material having refractive index mu=1.5. b...
Text Solution
|
- A rolling body is released from rest on sufficient rough long inclined...
Text Solution
|
- A uniform rod AB of mass m is suspended in equilibrium from two simila...
Text Solution
|
- Three perfect gases at absolute temperature T(1), T(2) and T(3) are mi...
Text Solution
|
- Assertion: The value of specific heat of a gas at constant pressure is...
Text Solution
|
- In Young's double slit experiment, the 10^(th) maximum of wavelength ...
Text Solution
|
- Consider two particles of equal mass m. If one particle is stationary ...
Text Solution
|
- Consider a force vecF = -xhati +yhatj. The particle is moved from poin...
Text Solution
|