A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
SAMPLE PAPER 4
EDUCART PUBLICATION|Exercise SECTION - B|20 VideosView PlaylistSAMPLE PAPER 3
EDUCART PUBLICATION|Exercise Section - C|7 VideosView PlaylistSAMPLE PAPER 6
EDUCART PUBLICATION|Exercise SECTION - C |9 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
EDUCART PUBLICATION-SAMPLE PAPER 4 -SECTION - C
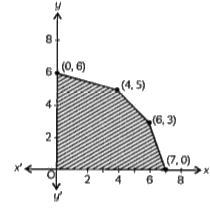
- The feasible region for an LPP is shown in the Let Z = 4x + 3y be the ...
02:05
|
Playing Now - On Sunday evening. Riya went to a nearby fair, which was set up every ...
03:00
|
Play - Differentiate tan^(-1)((sqrt(1-x^2))/x) with respect to cos^(-1)(2xsqr...
08:44
|
Play - For a square matrix of order 2, if A (adj A)= [{:(8,0),(0,8):}], then ...
01:49
|
Play - For the function if y = x ^(x ^(x^(x^----∞), then (dy)/(dx) is equal t...
03:16
|
Play - Case Study: The purpose of discipline in the workplace is to input of ...
01:42
|
Play - Case Study: The purpose of discipline in the workplace is to input of ...
03:51
|
Play