Home
Class 12
PHYSICS
A particle moves in the x-y plane with...

A particle moves in the x-y plane with a constant acceleration of `1.5m//s^(2)` in the direction making an angle of `37^(@)` with the x-axis.

At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.

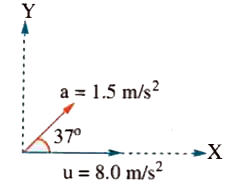
Text Solution

Verified by Experts

`13.3 m//s (41.6m, 7.2m)`
Promotional Banner

Topper's Solved these Questions

  • MOTION IN A PLANE

    AAKASH SERIES|Exercise QUESTION FOR DESCRIPTIVE ANSWER|7 Videos

  • MOTION IN A PLANE

    AAKASH SERIES|Exercise NUMERICAL EXERCISE (LEVEL -1)|33 Videos

  • MOTION IN A PLANE

    AAKASH SERIES|Exercise EXERCISE-3 (Circular Motion)|7 Videos

  • MOTION IN A STRAIGHT LINE

    AAKASH SERIES|Exercise very Short answer type question|15 Videos

Similar Questions

Explore conceptually related problems

A particle movesin the X-Y plane with a constasnt acceleration of 1.5 m/s^2 in the direction making an angle of 37^0 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

V_(x) is the velocity of a particle of a particle moving along the x- axis as shown. If x=2.0m at t=1.0s , what is the position of the particle at t=6.0s ?

A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)

a particle is moving in x-y-plane at 2 m//s along x-axis. 2 seconds later, its velocity is 4 m//s in a direction making 60^(@) with positive x-axis. Its average acceleration for the period of motion is:-

A time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m//s along negative x-axis at time t=0 . Find the velocity of the particle at the end of 4s.

The acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

Acceleration of particle moving along the x-axis varies according to the law a=-2v , where a is in m//s^(2) and v is in m//s . At the instant t=0 , the particle passes the origin with a velocity of 2 m//s moving in the positive x-direction. (a) Find its velocity v as function of time t. (b) Find its position x as function of time t. (c) Find its velocity v as function of its position coordinates. (d) find the maximum distance it can go away from the origin. (e) Will it reach the above-mentioned maximum distance?

A particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).

If the velocity of a particle moving along x-axis is given as v=(3t^(2)-2t) and t=0, x=0 then calculate position of the particle at t=2sec.

Starting from origin at t=0, with initial velocity 5 hat(j) m//s , a particle moves in the x-y plane with a constant acceleration of (10 hat(i) - 5hat(j))m//s^(2) . Find the coordinates of the particle at the moment its y-coordinate is maximum.

AAKASH SERIES-MOTION IN A PLANE-NUMERICAL EXERCISE (LEVEL -2)
  1. A shot is fired with a velocity u at a vertical wall whose distance f...

    Text Solution

    |

  2. An aeroplane flies horizontally at a height h at speed v. An anti - ca...

    Text Solution

    |

  3. Two guns situated at the top of a hill of height 10 m fire one shot ea...

    Text Solution

    |

  4. A particle projected with velcoity v(0) strikes at right alpha p...

    Text Solution

    |

  5. A particle moves in the x-y plane with a constant acceleration of...

    Text Solution

    |

  6. A particle moves in the x-y plane according to the law x=at, y=at (1-a...

    Text Solution

    |

  7. At the same instant two boy throw balls A and B from the window wit...

    Text Solution

    |

  8. A projectile aimed at a mark, which is in the horizontal plane through...

    Text Solution

    |

  9. Particles P and Q of mass 20 gm and 40 gm respectively are simultaneou...

    Text Solution

    |

  10. A particle is projected form point O on the ground with velocity u = s...

    Text Solution

    |

  11. A dip circle is at right angles to the magnetic meridian. What w...

    Text Solution

    |

  12. A glass wind screen whose inclination with the vertical can be changed...

    Text Solution

    |

  13. Two particles are projected from a point at the same instant with velo...

    Text Solution

    |

  14. Two boys simultaenously aim their guns at a brid sitting on a towe...

    Text Solution

    |

  15. A particle is projected with a velocity u making an angle theta with t...

    Text Solution

    |

  16. Figure shows a wire ring of radius a that is perpendicular to the gene...

    Text Solution

    |

  17. Two balls are projected from the same point in the direction inclined...

    Text Solution

    |

  18. Two particles are projected at the same instant from the same point ...

    Text Solution

    |

  19. A gun is kept on an inclined plane . The maximum ranges up and down ...

    Text Solution

    |