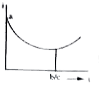
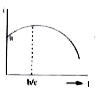
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
CURRENT ELECTRICITY
AAKASH SERIES|Exercise LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (More than one correct answer type Questions))|3 VideosView PlaylistCURRENT ELECTRICITY
AAKASH SERIES|Exercise LECTURE SHEET (EXERCISE- II LEVEL-I (MAIN) (Straight Objective Type Questions))|14 VideosView PlaylistCURRENT ELECTRICITY
AAKASH SERIES|Exercise EXERCISE - IA|2 VideosView PlaylistCURRENT ELECTRICITY
AAKASH SERIES|Exercise PROBLEMS (LEVEL-II)|27 VideosView PlaylistDUAL NATURE OF RADIATION AND MATTER
AAKASH SERIES|Exercise PRACTICE EXERCISEX|42 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
AAKASH SERIES-CURRENT ELECTRICITY-LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- The charge flowing in a conductor varies with time as Q= at -(1)/(2)bt...
03:19
|
Playing Now - Potential difference that is applied across a conductor of resistance ...
06:11
|
Play - An electric current passes through a circuit containing two wires of t...
02:29
|
Play - Two wires of the same material have length 6cm and 10cm and radii 0.5 ...
05:14
|
Play