Home
Class 10
MATHS
In the given figure ABC is a right angle...

In the given figure ABC is a right angled triangle with `angleB=90^(@) ` . D is the mid -point of BC . Show that `AC^(2) = AD^(2) +3CD^(2)` .

Answer

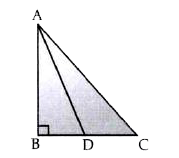
Step by step text solution for In the given figure ABC is a right angled triangle with angleB=90^(@) . D is the mid -point of BC . Show that AC^(2) = AD^(2) +3CD^(2) . by MATHS experts to help you in doubts & scoring excellent marks in Class 10 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • TRIANGLES

    OSWAL PUBLICATION|Exercise SELF ASSESSMENT -2 IV. ( LONG ANSWER TYPE QUESTIONS ) |3 Videos

  • TRIANGLES

    OSWAL PUBLICATION|Exercise SELF ASSESSMENT -2 VI. ( CASE STUDY BASED QUESTIONS ) |15 Videos

  • TRIANGLES

    OSWAL PUBLICATION|Exercise SELF ASSESSMENT -2 II. ( SHORT ANSWER TYPE QUESTIONS -I ) |3 Videos

  • SURFACE AREAS AND VOLUMES

    OSWAL PUBLICATION|Exercise BOARD CORNER (LONG ANSWER TYPE QUESTIONS)|9 Videos

Similar Questions

Explore conceptually related problems

In a triangle ABC,B=90^(@) and D is the mid-oint of BC then prove that AC^(2)=AD^(2)+3CD^(2)

In Delta ABC, angle B = 90^(@) and d is the mid - point of BC. Prove that AC ^(2) = AD^(2) + 3CD ^(2)

Knowledge Check

  • ABC is a right triangle with angleB=90^(@) and AC - AB = 1. If BC=sqrt(n) then AB is

    A
    `(n+1)/(2)`
    B
    `(n-1)/(2)`
    C
    `n/2`
    D
    `(n-3)/(2)`

  • If ABC is a right angled triangle at B and M, Nare the mid-points of AB and BC, then 4(AN^2+CM^2) is equal to :

    A
    `4AC^2`
    B
    `6AC^2`
    C
    `5AC^2`
    D
    `5/4AC^2`

    • Similar Questions

    Explore conceptually related problems

    In right-angled triangle ABC in which /_C=90^(@), if D is the mid-point of BC, prove that AB^(2)=4AD^(2)-3AC^(2)

    In Fig.3,ABC is a right triangle,right angled at C and D is the mid-point of BC.Prove that AB^(2)=4AD^(2)-3AC^(2)

    ABC is a right triangle with right angle at B, if P is a mid point of AC show that PB=PA=PC=(1)/(2)(AC)

    ABC is a right angled triangle in which angleB=90^(@) and AB=BC . Find angleA and angleC .

    In a right ABC right-angled at C, if D is the mid-point of BC, prove that BC^(2)=4(AD^(2)-AC^(2))

    In DeltaABC, angle A=90^(@), AB=AC, D is any point on BC. Provew that BD ^(2)+ CD^(2)=2AD^(2).

    Home
    Profile