Text Solution
Verified by Experts
|
Topper's Solved these Questions
NEWTON'S LAWS OF MOTION
HC VERMA|Exercise Short Answer|17 VideosView PlaylistNEWTON'S LAWS OF MOTION
HC VERMA|Exercise Objective 1|14 VideosView PlaylistNEWTON'S LAWS OF MOTION
HC VERMA|Exercise Exercises|42 VideosView PlaylistLAWS OF THERMODYNAMICS
HC VERMA|Exercise Short Answer|15 VideosView PlaylistPHYSICS AND MATHEMATICS
HC VERMA|Exercise Exercises|34 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
HC VERMA-NEWTON'S LAWS OF MOTION-Worked Out Examples
- A body of mass mis suspended by two strings making angles alpha and b...
05:25
|
Play - Two bodies of masses m1 and m2 are connected by a light string going ...
06:56
|
Play - A bullet moving at 250 m/s penetrates 5 cm into at tree limb before co...
02:48
|
Play - The force on a particle of mass 10 g is (veci10 + vecj5)N. If it start...
04:24
|
Play - With what acceleratin a should the box of figure desecend so that the ...
02:53
|
Play - A block A of mass m is tied to a fixed point C on a horizontal table t...
08:40
|
Play - A smooth ring A of mass m can slide on a fixed horizontal rod. A strin...
11:03
|
Play - A light rope fixed t one end of a wooden clamp on the ground passes ov...
05:11
|
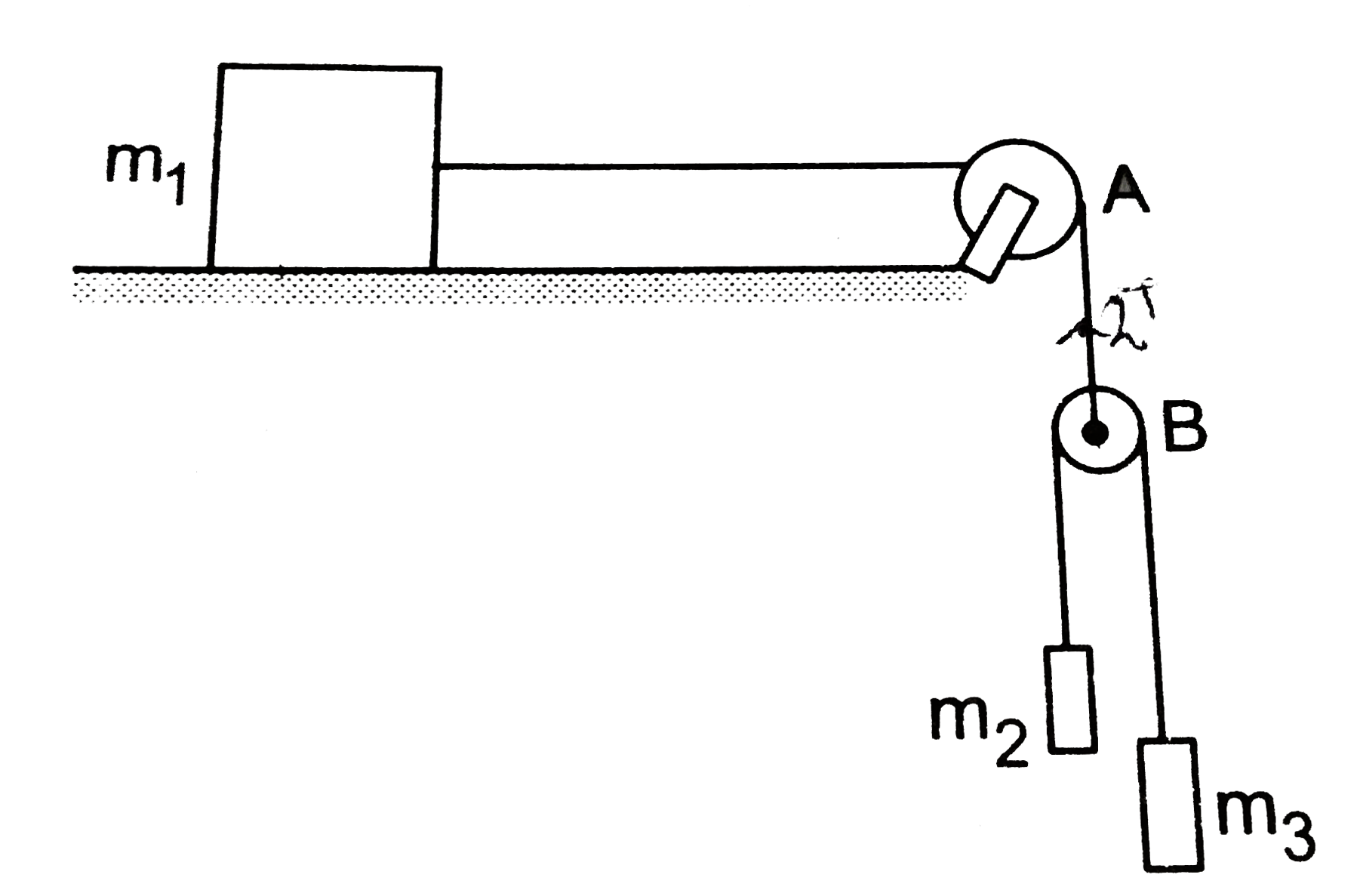
Play - Three blocks of masses m1, m2 and m3 are connected as shown in the fig...
11:57
|
Playing Now - A particle slides down a smooth in clined plane of elevation theta fix...
06:01
|
Play - All the surfaces shownin figure are assumed to be frictionless. The bl...
03:54
|
Play