Text Solution
Verified by Experts
|
Topper's Solved these Questions
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
HC VERMA|Exercise Objective 2|11 VideosView PlaylistCALORIMETRY
HC VERMA|Exercise Exercises|18 VideosView PlaylistCIRCULAR MOTION
HC VERMA|Exercise Exercises|30 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
HC VERMA-CENTRE OF MASS, LINEAR MOMENTUM, COLLISION-Exercises
- Solve tehh previous problem if the coefficient of restitution is e. Us...
Text Solution
|
Play - A block of mass 180 g is suspended by a massless spring. The spring ex...
06:59
|
Play - A bullet of mass 25 g is fired horizontally into a ballistic pendulum ...
04:51
|
Play - A bullet of mass 20 g moving horizontally at speed of 300 m/s is fire...
09:41
|
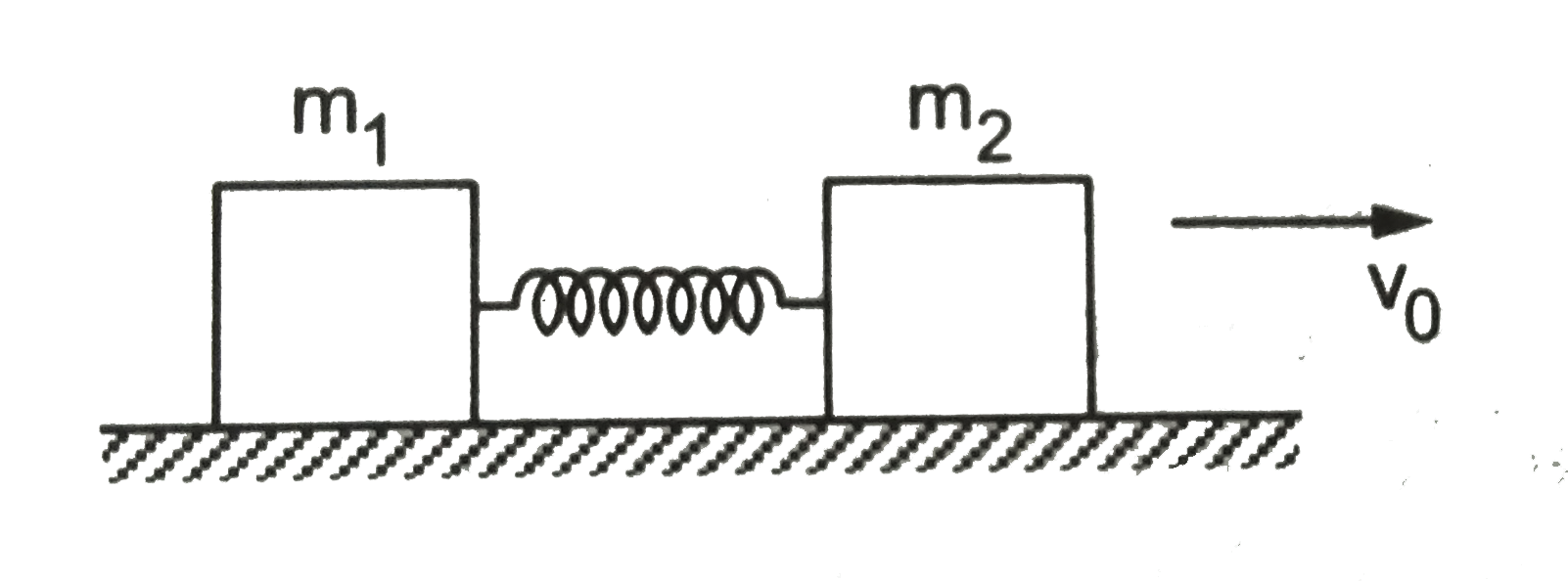
Play - Two masses m1 and m2 re connected by a spring of spring constnt k and ...
07:52
|
Play - Two blocks of masses m1 and m2 are connected by a spring of spring con...
05:08
|
Playing Now - Cionsider the situation of the previous problem. Suppose each of tbe b...
04:00
|
Play - consider the situastion of the previous problem. Suppose the block of ...
07:03
|
Play - Consider a gravity free hall in which an experimetner of mass 50 kg is...
09:47
|
Play - The track shown in figure is frictionles. The block B of mass 2m is ly...
08:55
|
Play - A bullet of mass 10 g moving horizontally at asped dof 50sqrt7m/s stri...
15:49
|
Play - Two balls having masses m and 2m are fastened to two light strings of ...
12:49
|
Play - A uniform chain of mass M and length L is held verticallyi in such a w...
07:44
|
Play - The blocks shown in figure have equal masses. The surface of A is smoo...
06:13
|
Play - The friction coefficient between the horizontal surface and each of th...
11:26
|
Play - A block of mas m is placed on a triangular block of mas m, which in tu...
10:14
|
Play - Figure shows a small body of mass m placed over a larger mass M whose ...
19:00
|
Play - A small block of superdennse material has a mass of 3xx10^24 kg. It i...
06:01
|
Play - A body of mass m makes an elastic collision with another identical bod...
11:31
|
Play - A small particle travelling with a velocity v collides elastically wit...
05:55
|
Play