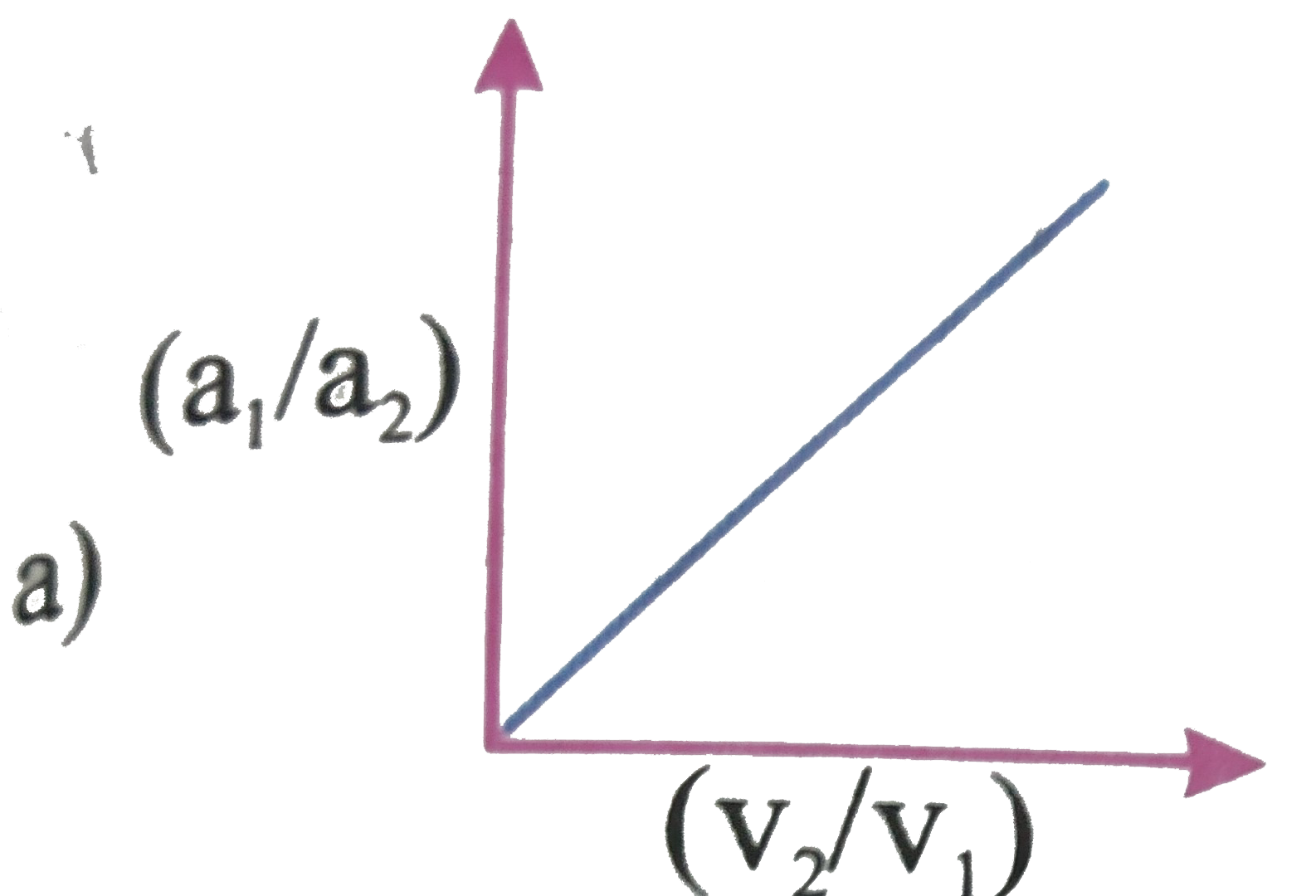
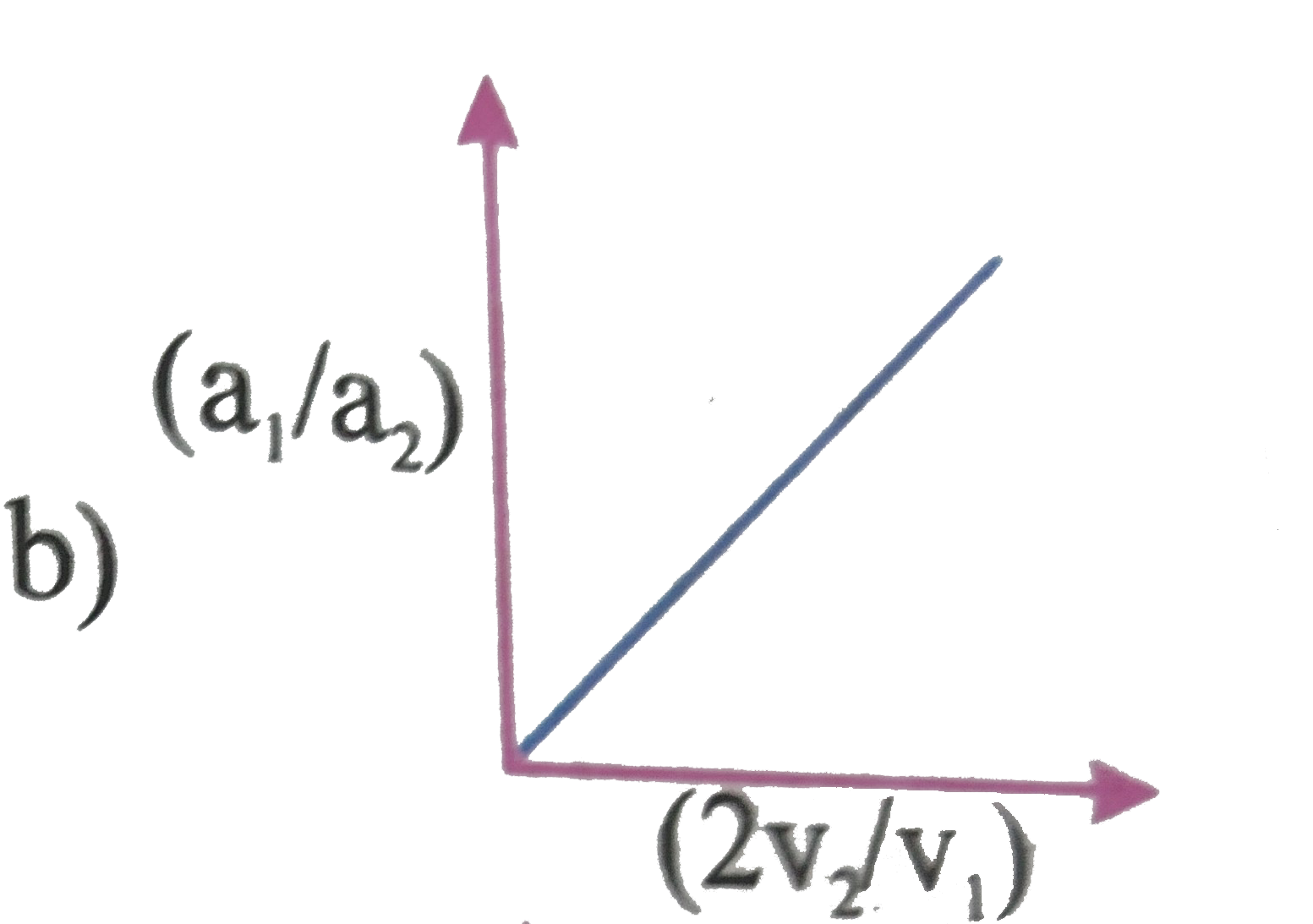
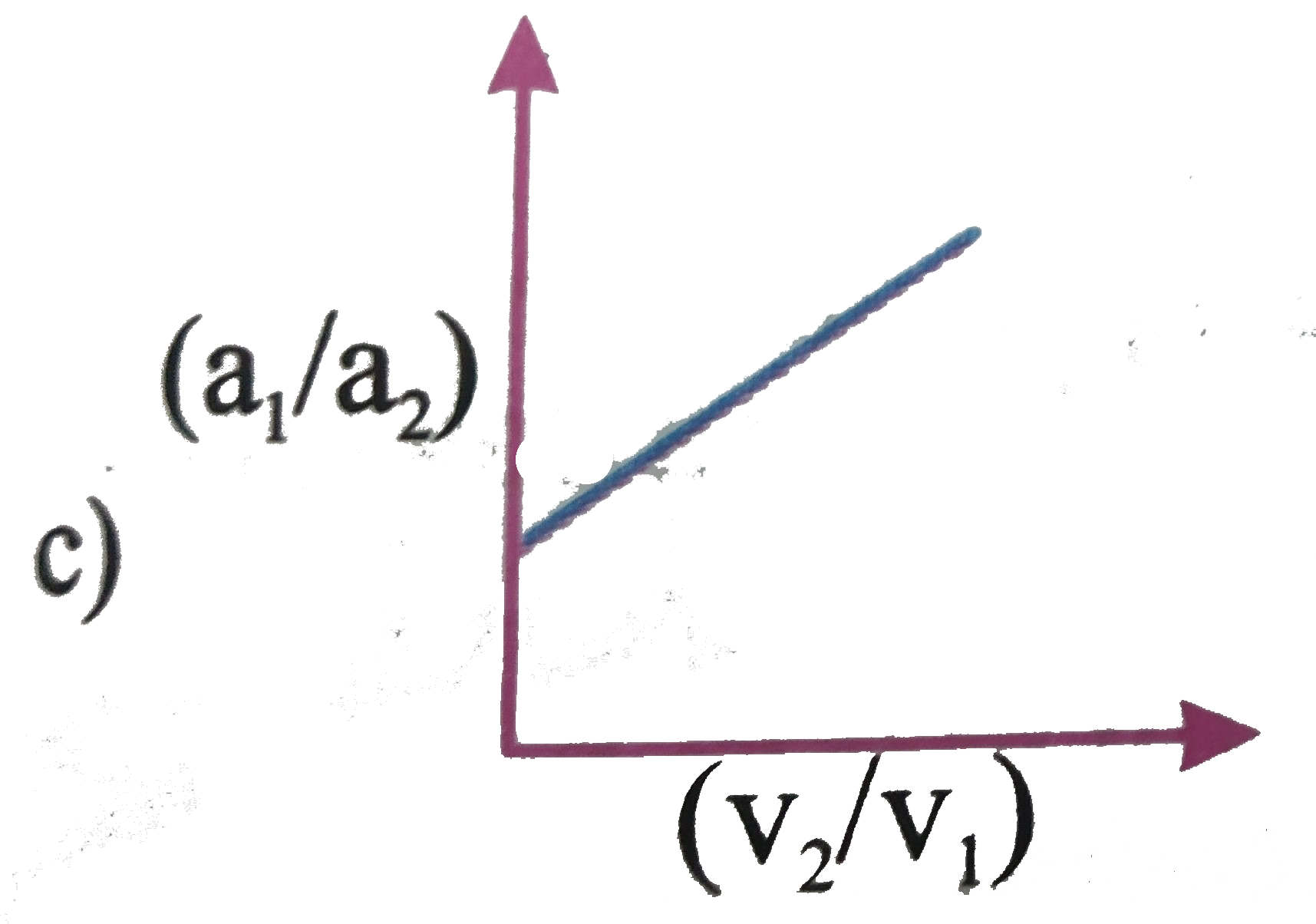
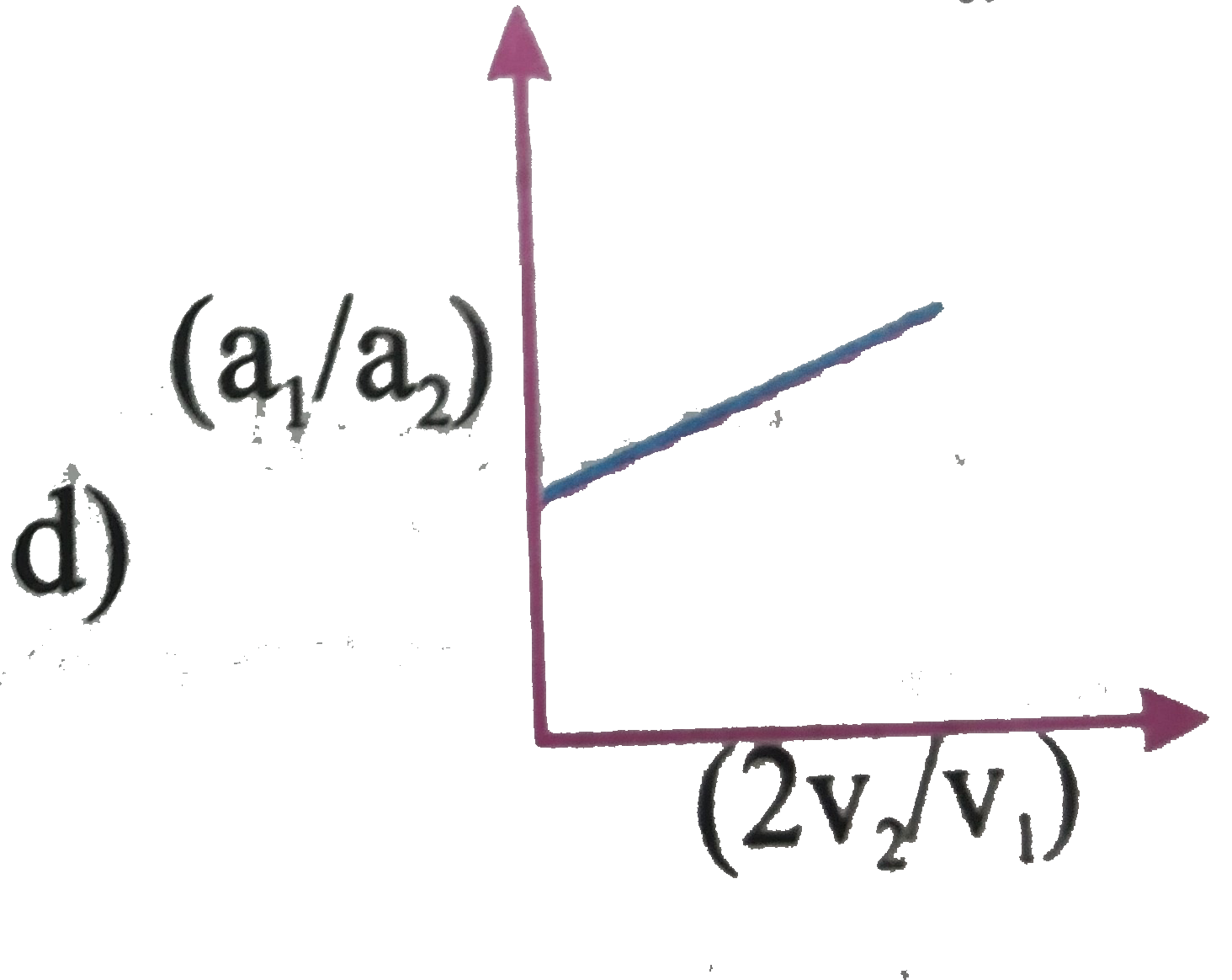A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
PRACTICE SET 17
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise PHYSICS & CHEMISTRY|50 VideosView PlaylistPRACTICE SET 19
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise Paper 1 (Physics & Chemistry)|50 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-PRACTICE SET 18-PAPER 1 (PHYSICS & CHEMISTRY)
- Three voltmeters A , B and C having resistances R, 1.5 R and 3R respec...
Text Solution
|
Play - A rectangular loop of sides 10cm and 5cm with a cut is stationary betw...
03:56
|
Play - A moving coil galvanometer has a resistance of 990Omega. in order to s...
03:19
|
Play - A particle is moving in circular path with constant acceleration. In t...
03:51
|
Play - A body floats in water with 40% of its volume outside water. When the ...
02:05
|
Play - A large open tank has two holes in its wall. Ine is a square hole of s...
03:09
|
Playing Now - A capillary tube of radius R is immersed in water and water rises in i...
02:24
|
Play - In Melde's experiment, the string vibrates in 4 loops when a 50 gram w...
03:37
|
Play - In Milikan's oil drop experiment, an oil drop of radius r and charge q...
02:24
|
Play - A conducting circular loop is placed in a uniform magnetic field 0.04T...
02:06
|
Play - A transistor is operated in common emitter configuration at V(c)=2 V s...
02:07
|
Play - Particle nature and wave nature of electromagnetic waves and electrons...
01:41
|
Play - A satellite is launched into a circular orbit of radius R around the e...
02:27
|
Play - A ray of light falls on a transparent glass slab of refractive index 1...
01:50
|
Play - A wire of natural length l, young's modulus Y and ares of cross-sectio...
02:20
|
Play - Two moles of oxygen are mixed with eight moles of helium. The effectiv...
02:10
|
Play - The wavelength of radiation emitted is lambda(0) when an electron jump...
03:08
|
Play - A particle executes simple harmonic motion with a period of 16s. At ti...
05:15
|
Play - A transparent plastic bag filled with air forms a concave lens. Now, i...
02:33
|
Play - The kinetic energy of an electron with de - Broglie wavelength of 0.3 ...
02:06
|
Play