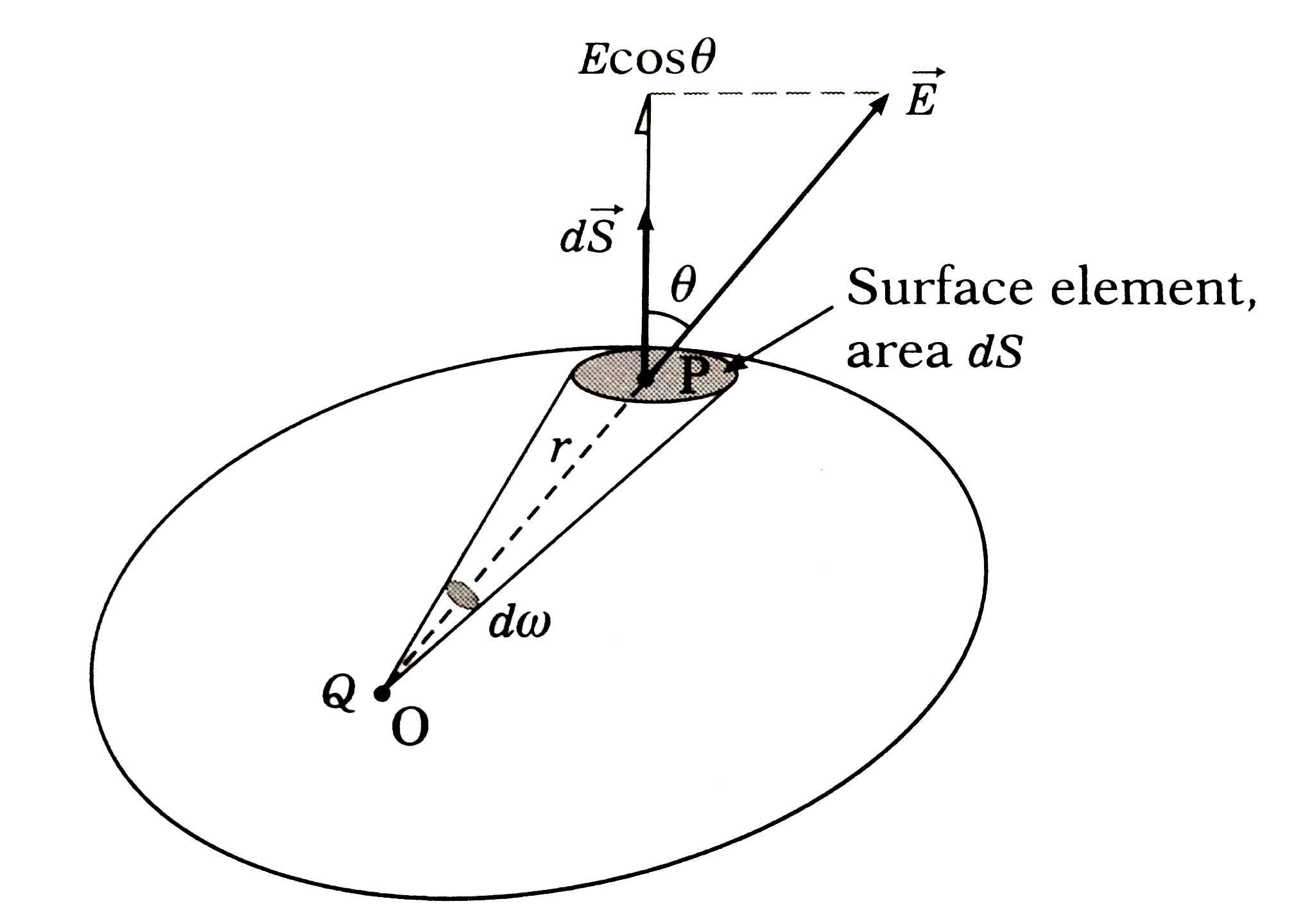Text Solution
Verified by Experts
Topper's Solved these Questions
DERIVATIONS-II
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Current Electricity|6 VideosDERIVATIONS-II
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Magnetism|1 VideosDERIVATIONS-II
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Interference and Diffraction|4 VideosDERIVATIONS-I
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assignments|9 VideosDISTINGUISH BETWEEN
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise Assingment|3 Videos
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-DERIVATIONS-II-Electrostatics
- State and prove Gauss's law in electrostatics.
Text Solution
|
- Derive an expression for the electric field intensity at a point outsi...
Text Solution
|
- Derive an expression for the electric field intensity at a point outsi...
Text Solution
|
- The mechanical force acting on a unit area of a charged conductor is
Text Solution
|
- Which of the following factors does not affect the mechanical force pe...
Text Solution
|
- Derive an expression for the capacitance of a parallel-plate capacitor...
Text Solution
|
- A dielectric of relative permittivity (dielectric constant ) k complet...
Text Solution
|
- What is the effect of presence of a dielectric medium on (i) capacit...
Text Solution
|
- Show that the enerty of a charged capacitor is (1)/(2)CV^(2). Also exp...
Text Solution
|
- Write different expression for the energy stored in a capacitor.
Text Solution
|
- Derive an expression for the effective capacitance of three capacitors...
Text Solution
|
- Derive an expression for the effective capacitance of three capacitors...
Text Solution
|