Home
Class 11
PHYSICS
A lamina is made by removing a small di...

A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is `I_O and I_P` respectively. Both these axes are perpendiucalr to the plane of the lamina. The ratio `I_P/I_O` ot the nearest integer is

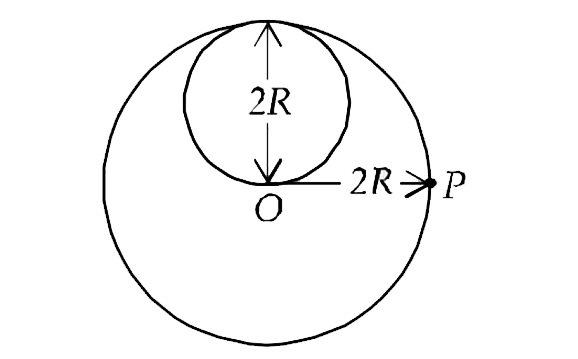
Text Solution

Verified by Experts

The correct Answer is:
C
Let `sigma` be the surface mass density. Then
`I_O = (1)/(2)sigma(2R)^2]xx(2R)^2 - `
`[(1)/(2)(sigmapiR^2)^2 + sigma(pi R^2)xxR^2]`
`=(13)/(2) pi sigma^4`
`I_P = 8pi sigma R^4 + sigma pi(2R)^2xx(2R)^2`
`[(1)/(2) sigma(pi R^2)R^2+sigma(piR^2)(sqrt((2R)^2+R^2))^2]`
`=24pi sigma R^4 - 5.5 sigma R^4 =18.5 pi sigma R^4`
`:. (I_P)/(I_O) = (18.5pi sigmaR^4)/(13)/(2) pi sigmaR^4 = (37)/(13) ~~3`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ROTATIONAL MOTION

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQs with one correct answer|1 Videos

  • MOTION

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|63 Videos

  • SIMPLE HARMONIC MOTION

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|69 Videos

Similar Questions

Explore conceptually related problems

A disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

A lamina is made by removing a small disc of diameter 2 R from a bigger disc of uniform mass density and radius 2R, as shown in figure. A second similar disc is made but instead of hole a disc of triple the density as of first it filled in the hole. Centre of mass is calculated in both the cases and was found at a distance r_(1) & r_(2) from centre O respectively find the ratio |(2r_(2))/(r_(1))|

Knowledge Check

  • A square lamina is as shown in figure. The moment of inertia of the frame about the three axes as shown in figure I_(1),I_(2) and I_(3) respectively. Select the correct alternative.

    A
    `I_(2)=I_(2) gt I_(1)`
    B
    `I_(1) gt I_(2) gt I_(3)`
    C
    `I_(2) = I_(3) lt I_(1)`
    D
    `I_(1) lt I_(2) lt I_(3)`

  • A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -

    A
    `4MR^(2)`
    B
    `9 MR^(2)`
    C
    `37/9MR^(2)`
    D
    `40/9MR^(2)`

  • From a disc of mass 2kg and radius 4m a small disc of radius 1 m with center O' is extracted . The new moment of inertia,about an axis passing through O perpendicular to plane of disc is

    A
    `16 kg m^(2)`
    B
    `12 kg m^(2)`
    C
    `( 255)/( 16) kg m^(2)`
    D
    `( 247)/( 16) kg m^(2)`

    • Similar Questions

    Explore conceptually related problems

    Mass of bigger disc having radius 2R is M. A disc of radius R is cut from bigger disc. Moment of intertia of disc about an axis passing through periphery and perpendicular to plane is

    A disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I = 1/(alpha) (31/3 m R^2) .

    The masses of two uniform discs are in the ratio 1 : 2 and their diameters in the ratio 2 : 1 . The ratio of their moment, of inertia about the axis passing through their respective centres and perpendicular to their planes is

    From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

    The diagram shows a uniform disc of mass M & radius ' a ', if the moment of inertia of the disc about the axis XY is I , its moment of inertia about an axis through O and perpendicular to the plane of the disc is

    Home
    Profile