Three infinitely long thin wires, each carrying current `i` in the same direction, are in the `x-y` plane of a gravity free space . The central wire is along the `y - axis` while the other two are along `x = +-d`.
(i) Find the locus of the points for which the magnetic field `B` is zero.
(ii) If the central wire is displaced along the ` Z- direction` by a small amount and released, show that it will excecute simple harmonic motion . If the linear density of the wires is `lambda`, find the frequency of oscillation.

Answer

A, B, C, D

Explanation

(i) KEY CONCEPT : Magnetic field due to an infinitely long current carrying wire at distance ` r` is given by
` B = (mu_(0))/(4pi) ((2i)/ (r ))`
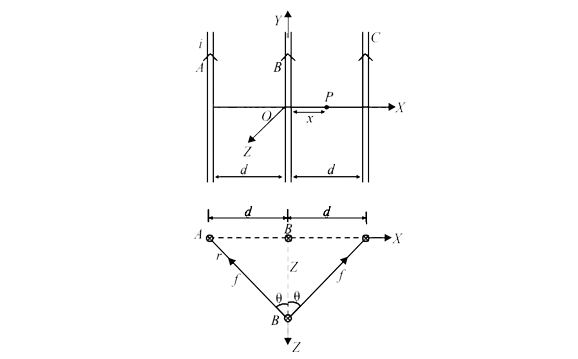
The direction of `B` is given by right hand palm rule. Hence , in case of three identical wires , resultant field can be zero only if the point `P` is between the two wires , otherwise `B` due to all the wires will be in the same direction and so resultant `B` cannot be zero. Hence , if point `P` is at a distance `x` from the central wire as shown in figure , then, ` vec(B)_(p) = vec(B)_(PA)+ vec(B)_(PC) `
where ` vec(B)_(PA) = magnetic field at p due to A `
` vec(B)_(PB) = magnetic field at P due to B`
` vec(B)_(PC) = magnet field at P due to C`.
`vec(B)_(P) = (mu_(0))/(4 pi)[ (1)/(d+x) + (1)/(x) - (1)/( d-x)] ( - hat(K))`.
For ` vec(B)_(P) = 0 `, we get ` x = +- d/ sqrt(3)`
(ii) KEY CONCEPT : the force per unit length between two parallel current carrying wires is given by
` (mu_(0))/( 4 pi) ( 2i_(1)i_(2))/ ( r ) = f(say)`
and i9s attractive if currents are in the same direction . ltbr. So , when the wire `B` is diplaced along ` Z- axis` by a small distance ` Z`, the restoring force per unit length `(F)/(l)` on the wire `B` due to wires `A and C` will be
` (F)/(l) = 2f cos theta =2 (mu_(0))/( 4pi) ( 2i_(1)i_(2))/( r ) xx(z) /( r ) [ as cos theta = (z)/( r ) ]`
or (F)/(l) = mu_(0) /( 4pi) . ( 4i^(2) z)/(( d^(2) + z^(2))) [ as I_(1) I_(2) and r^(2) = d^(2) + z^(2)]`
or (F)/(l) = mu_(0) /( 4pi) ( 2 i)/( d))^(2) z [ as d gtgt z and F is opposite to z]` .... (i)
Since `F prop -z`, the motion is simple harmonic.
Comparing eq. (i) with the standard equation of `S.H.M.` which is
` F = -m omega ^(2)z i.e. ,(F)/(l) = -(m)/(l) omega^(2)z` `= -lambda omega^(2) z`, we get
` lambda omega^(2) = (mu_(0))/( 4 pi) xx ( 4i^(2))/( d^(2)) rArr omega = sqrt ((mu_(0)i^(2))/( pi d^(2) lambda))`
` 2 pi n = (i)/(d)sqrt (( mu_(0))/( pi lambda)) rArr n = (i)/(2 pi d)sqrt((mu_(0))/( pi lambda)`