Home
Class 12
PHYSICS
A long current carrying wire , carrying ...

A long current carrying wire , carrying current `I_(1)` such that `I_(1)` is flowing out from the plane of paper is placed at `O`. A steady state current `I_(2)` is flowing in the loop `ABCD`

A

the net force is zero

B

the net torque is zero

C

as seen from `O` , the loop will rotate in clockwise along `OO'` axis

D

as seen from `O`, the loop will rotate in anticlockwise direction along `OO'` axis

Text Solution

Verified by Experts

The correct Answer is:
A, C
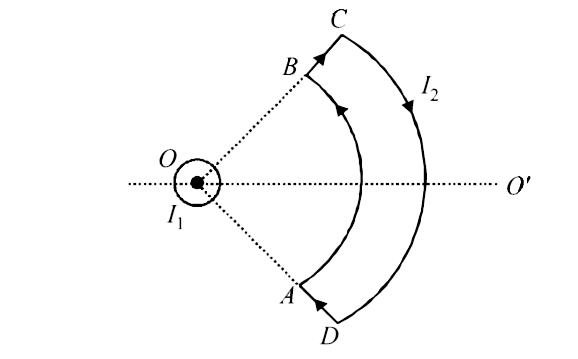
Net force on the loop :
Force on `AB` .
` dF xxBxx sin 0@) = 0`
Force on CD `: Similarly the magnetic field due to current `I_(1)` is along ` DC` . Because ` theta = 180^(@)` here , therefore force on ` DC` is zero .
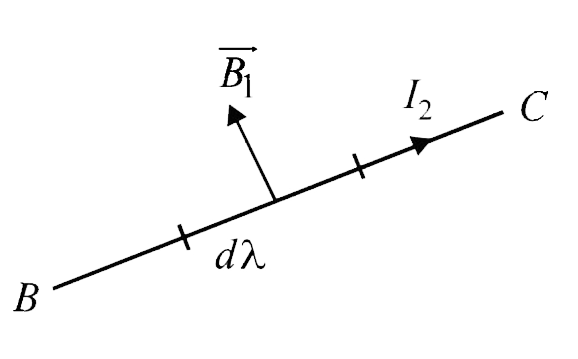
Force on `BC ` : Consider a small element `dl`.
` dF = I_(2) dl B_(1) sin 90^(@) rArr dF = I_(2) dl B_(1) `
By Fleming's left hand rule , the direction of this force is perpendicular to the plane of the paper directed outwards .
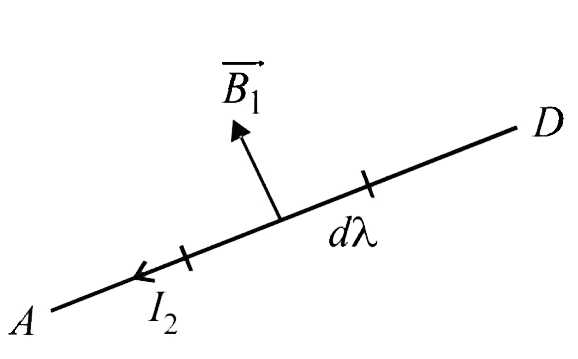
Force on ` AD` : ` dF = I_(2) dl B_(1) sin 90^(@) rArr dF = I_(2) dl B_(1) `
By Fleming's left hand rule , the direction of this force is perpendicular to the plane of paper directed inwards. Since the current elements are located symmetrical to current ` I_(1) , therfore force on `BC` will cancel out the effect of force on ` AD`.
rArr Net force on loop ` ABCD` is zero.
` NEt Torque on the loop : The force on ` BC and AD` will create a torque on ` ABCD` in clockwise direction about ` OO` as seen by the observer at `O`.


Promotional Banner

Topper's Solved these Questions

  • MOVING CHARGES AND MAGNETISM

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQs(d )|1 Videos

  • MODERN PHYSICS

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQ (One Correct Answer|1 Videos

  • RAY AND WAVE OPTICS

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|209 Videos

Similar Questions

Explore conceptually related problems

A long current carrying wire, carrying current such that it is flowing out from the plane of paper, is placed at O . A steady state current is flowing in the loop ABCD . Then

Figure shows a long straight current carrying wire with a current I_(1) and a thin strip of width b and length l placed parallel to it with a current I_(2) as shown in figure. Find the magnitude force of interaction between current I_(1) and I_(2)

A current loop ABCD is held fixed on the plane of the paper as shown in figure. The arcs BC( radius = b) and DA ( radius = a) of the loop are joined by two straight wires AB and CD at the origin O is 30^(@) . Another straight thin wire with steady current I_(1) flowing out of the plane of the paper is kept at the origin . The magnitude of the magnetic field (B) due to the loop ABCD at the origin (o) is :

A current loop ABCD is held fixed on the plane of the paper as shown in figure. The arcs BC( radius = b) and DA ( radius = a) of the loop are joined by two straight wires AB and CD at the origin O is 30^(@) . Another straight thin wire with steady current I_(1) flowing out of the plane of the paper is kept at the origin . Due to the process of the current I_(1) at the origin:

A long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is

A long straight wire is carrying current I in + z direction .The x-y plane contains a closed circular loop carrying current I_(2) and not encircling the straight wire.The force on the loop will be

A conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

Two long wire AB abd CD carry currents i_(1) and i_(2) in the direactions show in figure

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-MOVING CHARGES AND MAGNETISM-MCQs(d )
  1. A long current carrying wire , carrying current I(1) such that I(1) is...

    Text Solution

    |