Home
Class 12
PHYSICS
A cylindrical cavity of diameter a exist...

A cylindrical cavity of diameter a exists inside a cylinder of diameter `2a` as shown in the figure. Both the cylinder and the cavity are infinitity long. A uniform current density `j` flows along the length . If the magnitude of the magnetic field at the point `P` is given by `(N)/(12) mu_(0)aJ`, then the value of `N` is

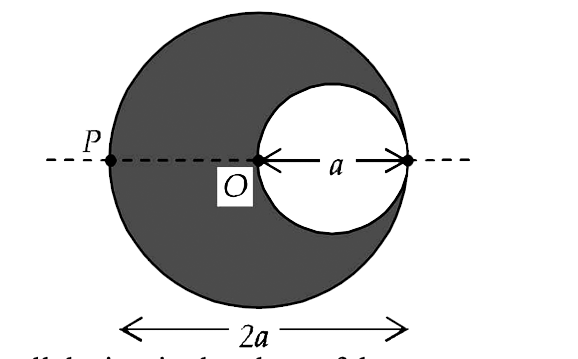
Text Solution

Verified by Experts

Current dwensity `J = ( current )/( area) = (I)/( pi( 2a^(2))) = (I')/( (pia^(2))`
rArr `I = (I') = (I)/(4)`
Let us consider the cavity to have current `I')` flowing in both the directions.
the magnetic field at `P` due to the current flowing through the cylinder
` B_(1) = (mu_(0))/( 4 pi) ( 2I)/(a)`
The magnetic field at `P` due to the current `( I')` flowing in opposite direction is
` B_(2) = (mu_(0))/( 4 pi) (3I')/( 3a//2) = ( mu_(0))/( 4 pi) (2(I//4))/(3a//2) = (mu_(0))/( 4 pi) (I)/( 3a)`
:. The net magnetic field is
`B = B_(1) - B_(2) = (mu_(0))/( 4 pi) (I)/(a)[ 2 - (1)/(3)] = (mu_(0))/(4 pi) (I)/(a)xx(5)/(3)
:. `(B = mu_(0))/( 4 pi) (J pi a^(2))/(a)xx(5)/(3) = mu_(0) ( 5 Ja)/(12)
Promotional Banner

Topper's Solved these Questions

  • MOVING CHARGES AND MAGNETISM

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQs(d )|1 Videos

  • MODERN PHYSICS

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQ (One Correct Answer|1 Videos

  • RAY AND WAVE OPTICS

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|209 Videos

Similar Questions

Explore conceptually related problems

A cylinderical cavity of diameter a exists inside a cylinder of diameter 2a as shown in the figure. Both the cylinder and the cavity are infinitely long. A uniform current density J flows along the length. If the magnitude of the magnetic field at the point P is given by (N)/(12)mu_(0)aJ , then the value of N is

A hollow cylinder having infinite length and carrying unifrom current per unit length lamda along the circumference as shown Magnetic field inside the cylinder is .

A current I(=4A) flows along a thin wire PQRS shaped as shown in figure. The radius of the curved part of the wire is 10*0cm . The angle theta=90^@ . Find the magnitude of the total magnetic field at the point O.

An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius (R)/(2) are shown in the figure. The remaining portion has uniform volume charge density rho . The magnitude of electrical field at the centre of the cavity is-

Two infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is

A thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.

An infinitely long hollow coducting cylinder with inner radius R/2 and outer radus R carries a uniform current density along its length. The magnitude of the magnetic field |B| as a function of the radial distance r from the axis is best represented by

An infinitely long hollow conducting cylinder with inner radius (R )/(2) and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , | vec(B)| as a function of the radial distance r from the axis is best represented by

A cylinder of radius R_(1) have cylinderical cavity of radius R_(2) as shown in the figure and have current density J (down ward). Find Magnetic field when when point is in cavity