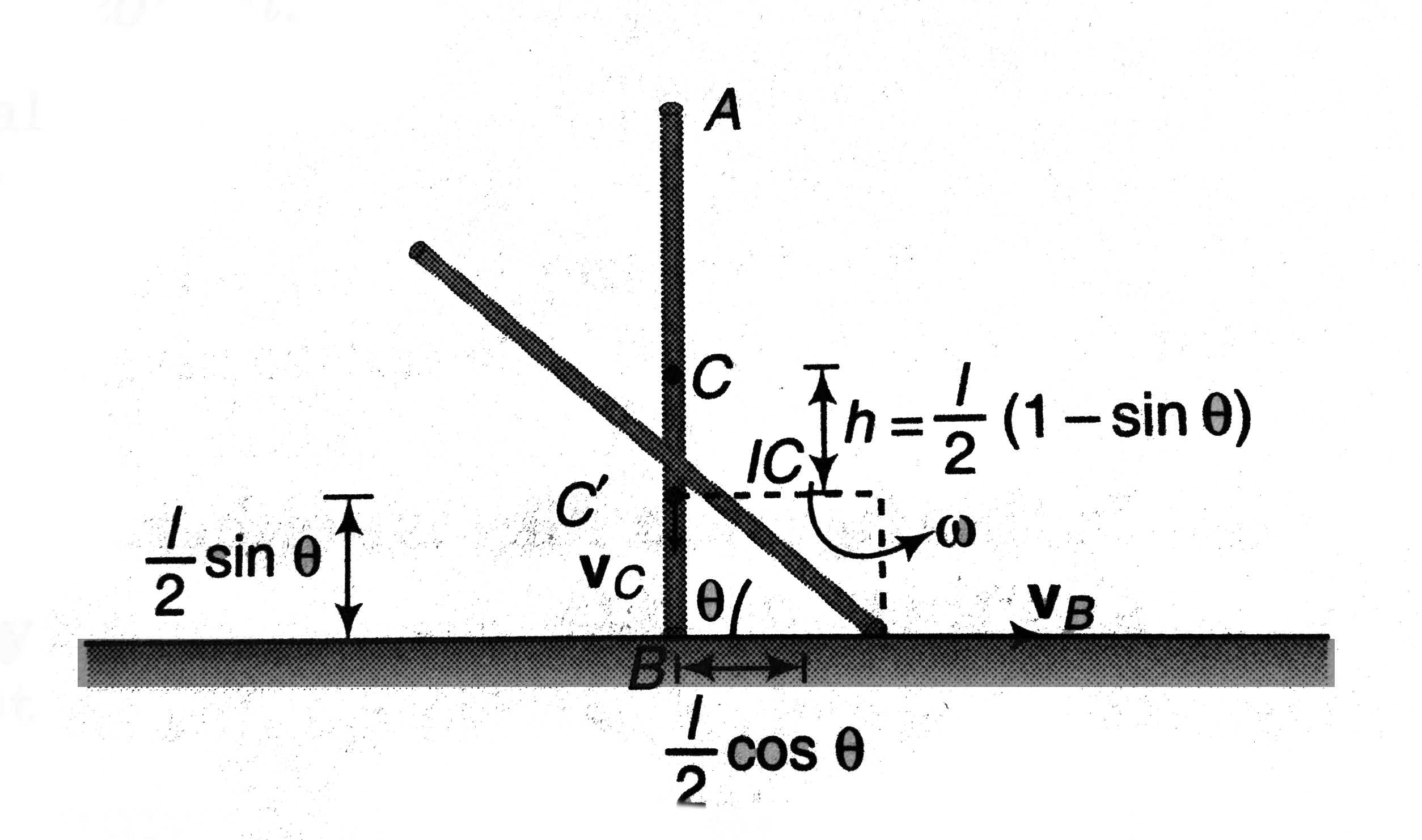Text Solution
Verified by Experts
|
Topper's Solved these Questions
ROTATIONAL MECHANICS
DC PANDEY|Exercise Miscellaneous Examples|2 VideosView PlaylistROTATIONAL MECHANICS
DC PANDEY|Exercise Solved Example|1 VideosView PlaylistROTATIONAL MECHANICS
DC PANDEY|Exercise Subjective Questions|2 VideosView PlaylistROTATION
DC PANDEY|Exercise (C) Chapter Exercises|39 VideosView PlaylistROTATIONAL MOTION
DC PANDEY|Exercise Integer Type Questions|17 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
DC PANDEY-ROTATIONAL MECHANICS-Solved Examples
- Repeat all parts of above problem for F=40N
07:09
|
Play - A solid cylinder of mass m and radius r starts rolling down an incline...
03:38
|
Play - A small solid cylinder of radius r is released coaxially from point A ...
08:25
|
Play - A small object of uniform density rolls up a curved surface with an in...
03:43
|
Play - A solid ball rolls down a parabolic path ABC from a height h as shown ...
08:03
|
Play - A ball moves over a fixed track as shown in thre figure. From A to B t...
04:57
|
Play - A small solid sphere of mass m is released from point A. portion AB is...
11:52
|
Play - A rotating disc moves in the positive direction of the x-axis. Find th...
05:30
|
Play - A uniform thin rod of mass m and length l is standing on a smooth hori...
07:45
|
Playing Now - In the arrangement shown in figure the mass of the uniform solid cylin...
07:47
|
Play - solid sphere of radius r is gently placed on a rough horizontal ground...
04:00
|
Play - A billiard ball, initially at rest, is given a sharp impulse by a cue....
15:20
|
Play - For the given dimensions shown in figure, find critical value of coeff...
03:50
|
Play - In the figure shown in the text, if the block is a cube of side a fi...
15:55
|
Play - Consider the arrangement shown in figure. The string is wrapped around...
04:26
|
Play - A thin massless thread is wound on a reel of mass 3 kg and moment of i...
11:23
|
Play - A body of mass m, radius R and moment of inertia I (about an axis pass...
04:38
|
Play - In the figure given in the text if mass of the rod is m then find hing...
05:43
|
Play - Two uniform thin rods A and B of length 0.6 m each and of masses 0.01 ...
09:23
|
Play - A rod AB of mass M and length L is lying on a horizontal frictionless ...
09:40
|
Play