Home
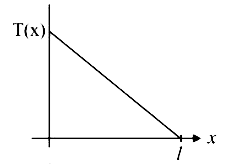
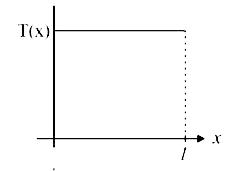
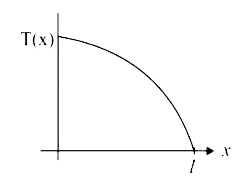
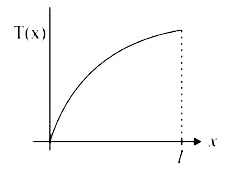
Class 11
PHYSICS
A uniform rod of mass m and length l rot...

A uniform rod of mass `m` and length `l` rotates in a horizontal plane with an angular velocity `omega` about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is

A

`(1)/(2)momega^(2)x`

B

`(1)/(2)momega^(2)(1-(x^(2))/(l))`

C

`(1)/(2)momega^(2)l(1-(x^(2))/(l^(2)))`

D

`(1)/(2)momega^(2)l[1-(x)/(l)]`

Text Solution

AI Generated Solution

To find the tension in a uniform rod of mass `m` and length `l` rotating in a horizontal plane with an angular velocity `ω` about a vertical axis passing through one end, we can follow these steps: ### Step-by-Step Solution: 1. **Understanding the System**: - We have a uniform rod of length `l` and mass `m` rotating about a vertical axis at one end with angular velocity `ω`. We need to find the tension in the rod at a distance `x` from the axis of rotation. 2. **Identifying the Element of the Rod**: ...
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ROTATIONAL MECHANICS

    DC PANDEY|Exercise Level 2 Multiple Correct|36 Videos

  • ROTATIONAL MECHANICS

    DC PANDEY|Exercise Level 2|1 Videos

  • ROTATIONAL MECHANICS

    DC PANDEY|Exercise Level 1 Subjective|32 Videos

  • ROTATION

    DC PANDEY|Exercise (C) Chapter Exercises|39 Videos

  • ROTATIONAL MOTION

    DC PANDEY|Exercise Integer Type Questions|17 Videos

Similar Questions

Explore conceptually related problems

A uniform rod of mass m and length l_(0) is rotating with a constant angular speed omega about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle theta to the vertical (axis of rotation).

A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.

Knowledge Check

  • A thin uniform rod of mass m and length L rotates with the constant angular velocity omega about .the vertical axis passing through the rod's suspensjon point O . It describes a carried surface, then:

    A
    centrifugal force acting on rod is `m L/2 sin theta omega^(2)` and will pass through centre of mass
    B
    centrifugal force acting on rod is `m L/2 sin theta omega^(2)` and will not pass through centre of mass
    C
    `theta=cos^(-1)((3g)/(2omega^(2)L))`
    D
    `theta=cos^(-1)(g/(omega^(2)L))`

  • A uniform rod of length l is being rotated in a horizontal plane with a constant angular speed about an axis passing through one of its ends. If the tension generated in the rod due to rotation is T(x) at a distance x from the axis, then which of the following graphs depicts it most closely ?

    A
    B
    C
    D

  • A thin uniform copper rod length l and mass m rotates unifomly with an angular velocity omega about a vertical axis passing through one of its ends as shown in the figure. Young's modulus of copper is Y. Breaking stress is sigma_(max) , cross sectional area of rod is A and density of rod is uniform. Based on above information, answer the following questions The maximum angular velocity with which the rod can rotate so that is won't break, is

    A
    `sqrt((2sigma_(max)A)/(ml))`
    B
    `sqrt((2sigma_(max)A)/(3ml))`
    C
    `sqrt((sigma_(max)A)/(2ml))`
    D
    `sqrt((3sigma_(max)A)/(ml))`

    • Similar Questions

    Explore conceptually related problems

    A thin uniform rod of length l and masses m rotates uniformly with an angularly velocity omega in a horizontal plane about a verticle axis passing through one of its ends determine the tension in the rot as a funtion of the distance x from the rotation axis

    A smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.

    A rod AB of length l is pivoted at an end A and freely rotated in a horizontal plane at an angular speed omega about a vertical axis passing through A. If coefficient of linear expansion of material of rod is alpha , find the percentage change in its angular velocity if temperature of system is incresed by DeltaT

    A rigid rod of mass m and lengths l, is being rotated in horizontal plane about a vertical axis, passing through one end A. If T_(A), T_(B) and T_(C) are the tensions in rod at point A, mid point B and point C of rod repsectively, then

    A uniform rod of mass m and length L lies radialy on a disc rotating with angular speed omega in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

    Home
    Profile