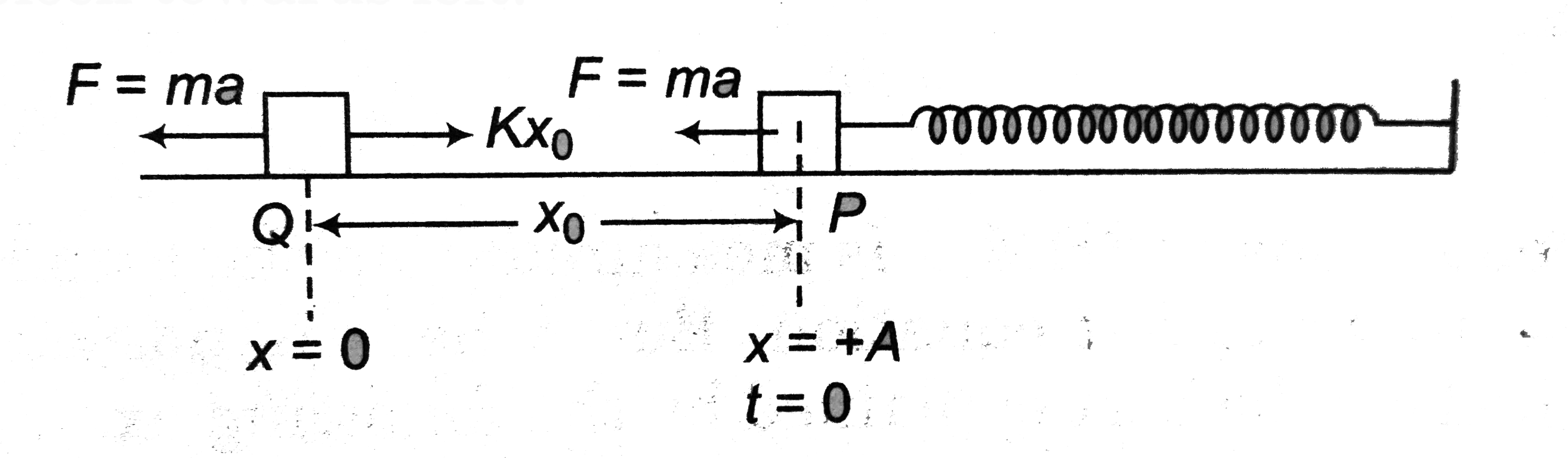Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
DC PANDEY|Exercise Example Type 10|1 VideosView PlaylistSIMPLE HARMONIC MOTION
DC PANDEY|Exercise Example Type 11|2 VideosView PlaylistSIMPLE HARMONIC MOTION
DC PANDEY|Exercise Example Type 8|1 VideosView PlaylistSEMICONDUCTORS AND ELECTRONIC DEVICES
DC PANDEY|Exercise More than One Option is Correct|3 VideosView PlaylistSOLVD PAPERS 2017 NEET, AIIMS & JIPMER
DC PANDEY|Exercise Solved paper 2018(JIPMER)|38 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems