Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
WAVE MOTION
DC PANDEY|Exercise Subjective Questions|2 VideosView PlaylistWAVE MOTION
DC PANDEY|Exercise JEE MAINS|50 VideosView PlaylistWAVE MOTION
DC PANDEY|Exercise Level 2 More Than One Correct|6 VideosView PlaylistVECTORS
DC PANDEY|Exercise Medical enrances gallery|9 VideosView PlaylistWORK, ENERGY & POWER
DC PANDEY|Exercise Level 2 Comprehension Based|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
DC PANDEY-WAVE MOTION-Level 2 Subjective
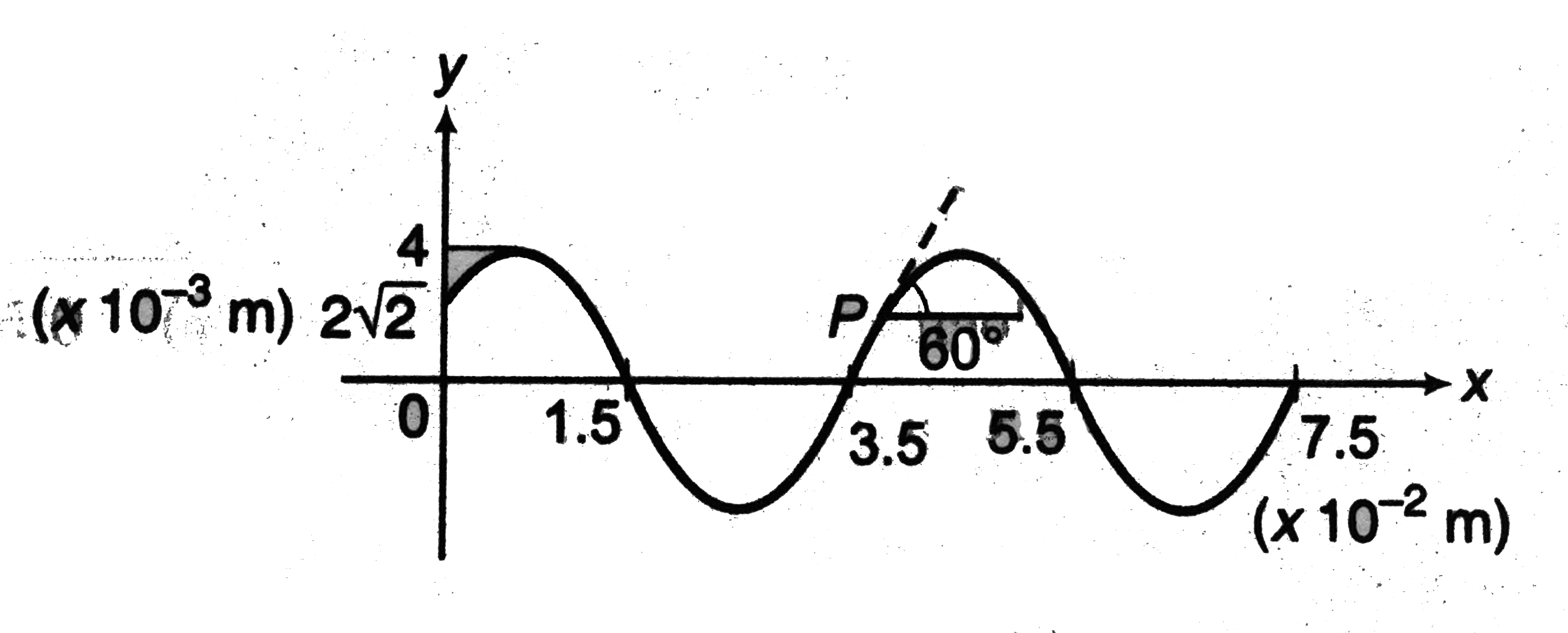
- The figure shows a snap photograph of a vibrating string at t = 0. The...
06:45
|
Playing Now - A long string having a cross- sectional area 0.80 mm^2 and density 12....
10:27
|
Play - One end of each of two identical springs, each of force constant 0.5N/...
04:43
|
Play - A wave pulse is travelling on a string with a speed v towards the posi...
04:21
|
Play - Figure shows a plot of the transverse displacement of the particle of ...
02:31
|
Play - Two wires of different densities but same area of cross-section are so...
01:42
|
Play - A sinusoidal transverse wave travel on a string. The string has length...
03:25
|
Play