Home
Class 11
PHYSICS
One end of the rod of length l, thermal ...

One end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of `100^@C`. At the other end large quantity of ice is kept at `0^@C` . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
.

Text Solution

Verified by Experts

The correct Answer is:
A, D
Putting,
`((dQ)/dt)_("conduction")=((dQ)/(dt))_("calorimetry")`
`:. (TD)/R = L* (dm)/(dt)`
`rArr (dm)/(dt) = (TD)/(RL)`
So, this is the desired expression of `(dm)/(dt)`.
In the above expression,
`TD = 100^@C, R = l/(KA)`
and L = latent heat of fusion.
Promotional Banner

Topper's Solved these Questions

  • CALORIMETRY & HEAT TRANSFER

    DC PANDEY|Exercise Example Type 3|1 Videos

  • CALORIMETRY & HEAT TRANSFER

    DC PANDEY|Exercise Example Type 4|4 Videos

  • CALORIMETRY & HEAT TRANSFER

    DC PANDEY|Exercise Example Type 1|4 Videos

  • BASIC MATHEMATICS

    DC PANDEY|Exercise Exercise|13 Videos

  • CALORIMETRY AND HEAT TRANSFER

    DC PANDEY|Exercise Medical entrance s gallery|38 Videos

Similar Questions

Explore conceptually related problems

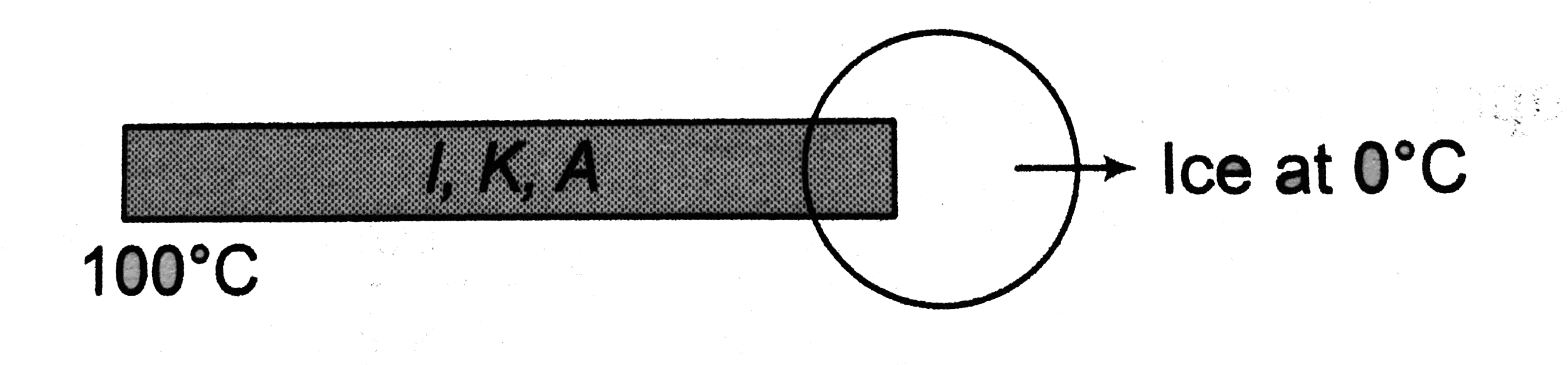One end of conducting rod is maintained at temperature 50^(@)C and at the other end ice is melting at 0^(@)C . The rate of melting of ice is doubled if:

The end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4 cal//s . Then, in the second rod rate of heat flow in cal//s will be

One end of a copper rod of length 1 m and area of cross - section 400 xx (10^-4) m^2 is maintained at 100^@C . At the other end of the rod ice is kept at 0^@C . Neglecting the loss of heat from the surrounding, find the mass of ice melted in 1h. Given, K_(Cu) = 401 W//m-K and L_f = 3.35 xx (10^5) J//kg.

The ends of a copper rod of length 1m and area of cross-section 1cm^2 are maintained at 0^@C and 100^@C . At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400 Wm^-1 K^-1 .

A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T_(0) and the furnace is maintained at T_(1) = T_(0) + DeltaT_(1) . The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T_(2) = T_(0) + DeltaT_(2) [DeltaT_(2) ltlt T_(0)] . The exposed surface of the rod has emissivity e. Prove that DeltaT_(1) is proportional to DeltaT_(2) and find the proportionality constant.

One end of a metal rod of length 1.0 m and area of cross section 100 cm^(2) is maintained at . 100^(@)C . If the other end of the rod is maintained at 0^(@)C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod = 100 W//m-K )

The ends of the two rods of different materials with their lengths, diameters of cross-section and thermal conductivities all in the ratio 1 : 2 are maintained at the same temperature difference. The rate of flow of heat in the shorter rod is 1cals^(-1) . What is the rate of flow of heat in the larger rod:

Two rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .

Two ends of area A of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. At any point on the rod, the temperature gradient is (dT)/(dl) . If I be the thermal current in the rod, then:

The two ends of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. The temperature gradientat any point on the rod is (d theta)/(dl) (equal to the difference in temperature per unit length). The heat flow per unit time per unit cross-section of the rod is l then which of the following statements is/are correct: