Consider a simple harmonic progressive wave travelling with a speed v along the positive x-axis. Let y denote the displacement of a particle of the medium from its mean position. At time t, the displacement of the particle of the medium situated at the origin is
`y=A sin omegat " "`.....(1)
assuming that the epoch is zero. A is the amplitude of the wave and `omega=2pin`, where n is the frequency of the wave motion.
Consider a particle of the medium situated at point P at a distance x from the origin O as shown in the figure. This particle also performs SHM with the same amplitude A and the frequency n. Hoever, the disturbance at O reaches P only after some time. Hence, the particle at P lags behind the particle at O in phase. If `alpha` denotes the phase lag, the displacement of the particle at P is
`y=A sin (omega t-alpha)" "`....(2)
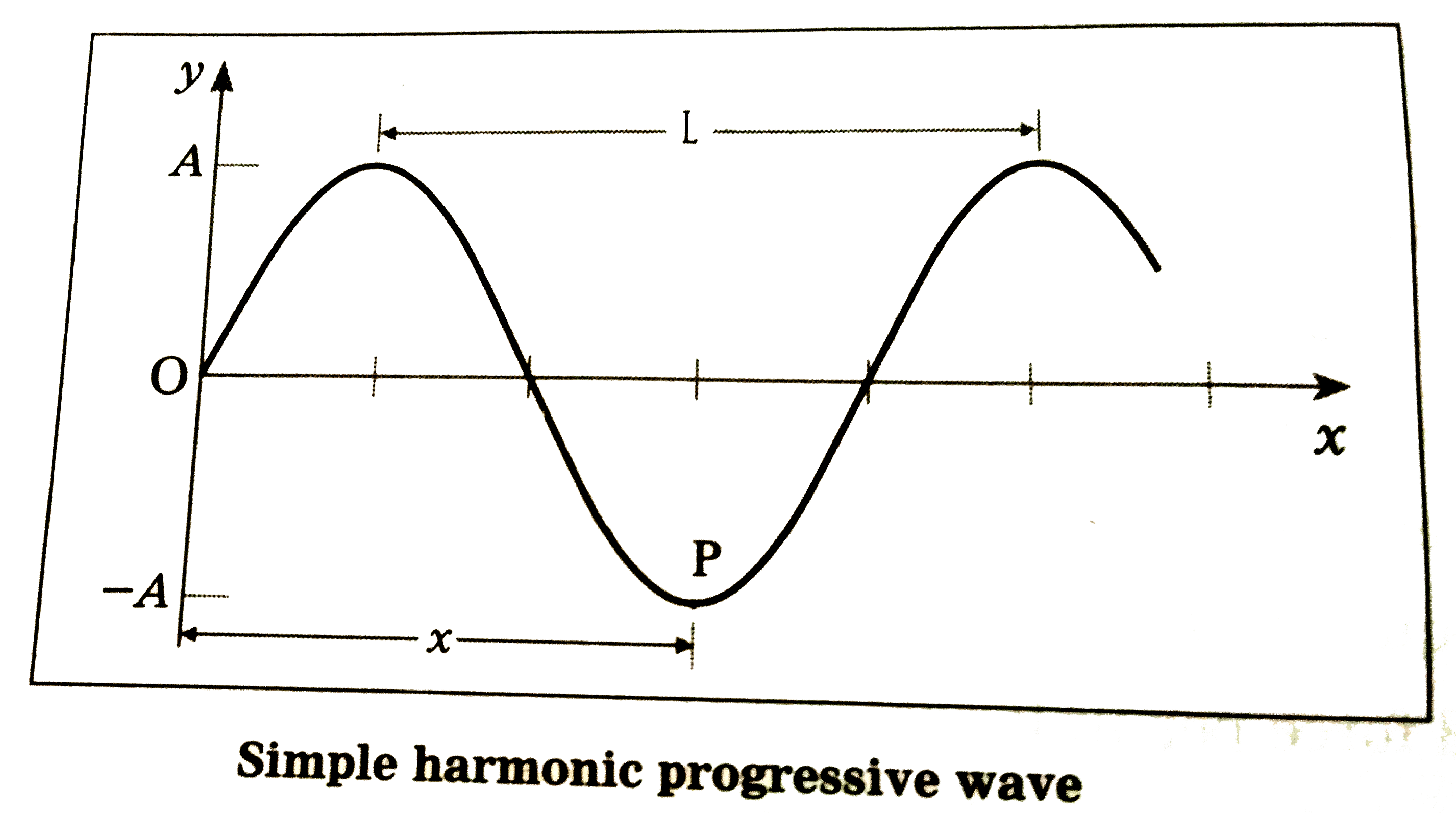
Since a path difference of one wavelength `(lambda)` corresponds to a phase difference of `2pi` radians, a path difference of x corresponds to a phase difference of `(2pi)/(lambda)`x radian. Thus, `alpha=(2pi)/(lambda)x`.
`:. y=A sin (omegat-(2pi)/(lambda)x)" "`....(3)
If T is the period of vibrations, `omega=(2pi)/(T)`.
`:. y=A sin ((2pit)/(T)-(2pi)/(lambda)x)`
`:. y=A sin 2pi((t)/(T)-(x)/(lambda))" "`.....(4)
Equation (4) is the equation of a simple harmonic progressive wave travelling in the positive direction of the x-axis.
The frequency of vibrations, `n=(1)/(T)`. Therefore, from Eq. (3),
`y=A sin 2pi(nt-(x)/(lambda))" "`.....(5)
`:. y=A sin 2pin(t-(x)/(nlambda))`
But `nlambda=v`, the speed of the wave.
`:. y=A sin 2pi n(t-(x)/(v))" "`....(6)
Equations (5) and (6) are the other two different forms of the equation of a simple harmonic progressive wave.
[Note : Also, writing `n=(v)/(lambda)` in Eq. (6), we get,
`y=A "sin" (2pi)/(lambda)(vt-x)" "`....(7)
The quantity `2pi//lambda=k` is called the propagation constant.
Substituting `k=2pi//lambda` in Eq. (1), we get,
`y=A sin (omegat-kx)" "`.....(8)
Equations (7) and (8) are two additional forms of the equation of a simple harmonic progressive wave.]
