Text Solution
Verified by Experts
|
Topper's Solved these Questions
KINEMATICS-1
CENGAGE PHYSICS|Exercise Solved Examples|9 VideosView PlaylistKINEMATICS-1
CENGAGE PHYSICS|Exercise Exercise 4.1|17 VideosView PlaylistGRAVITATION
CENGAGE PHYSICS|Exercise INTEGER_TYPE|1 VideosView PlaylistKINEMATICS-2
CENGAGE PHYSICS|Exercise Exercise Integer|9 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-KINEMATICS-1-Integer
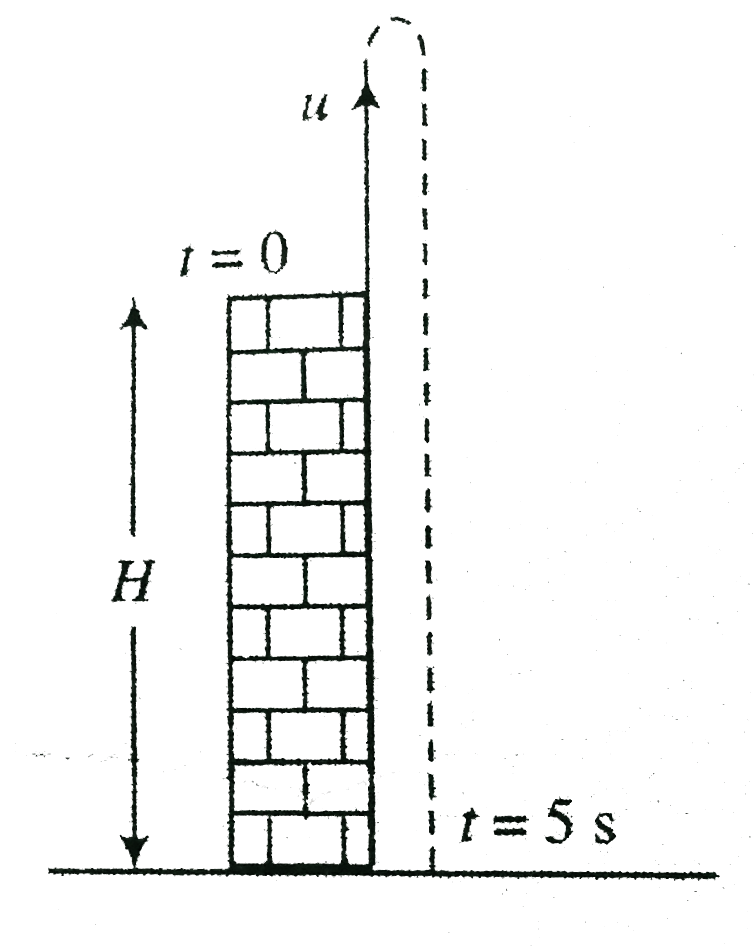
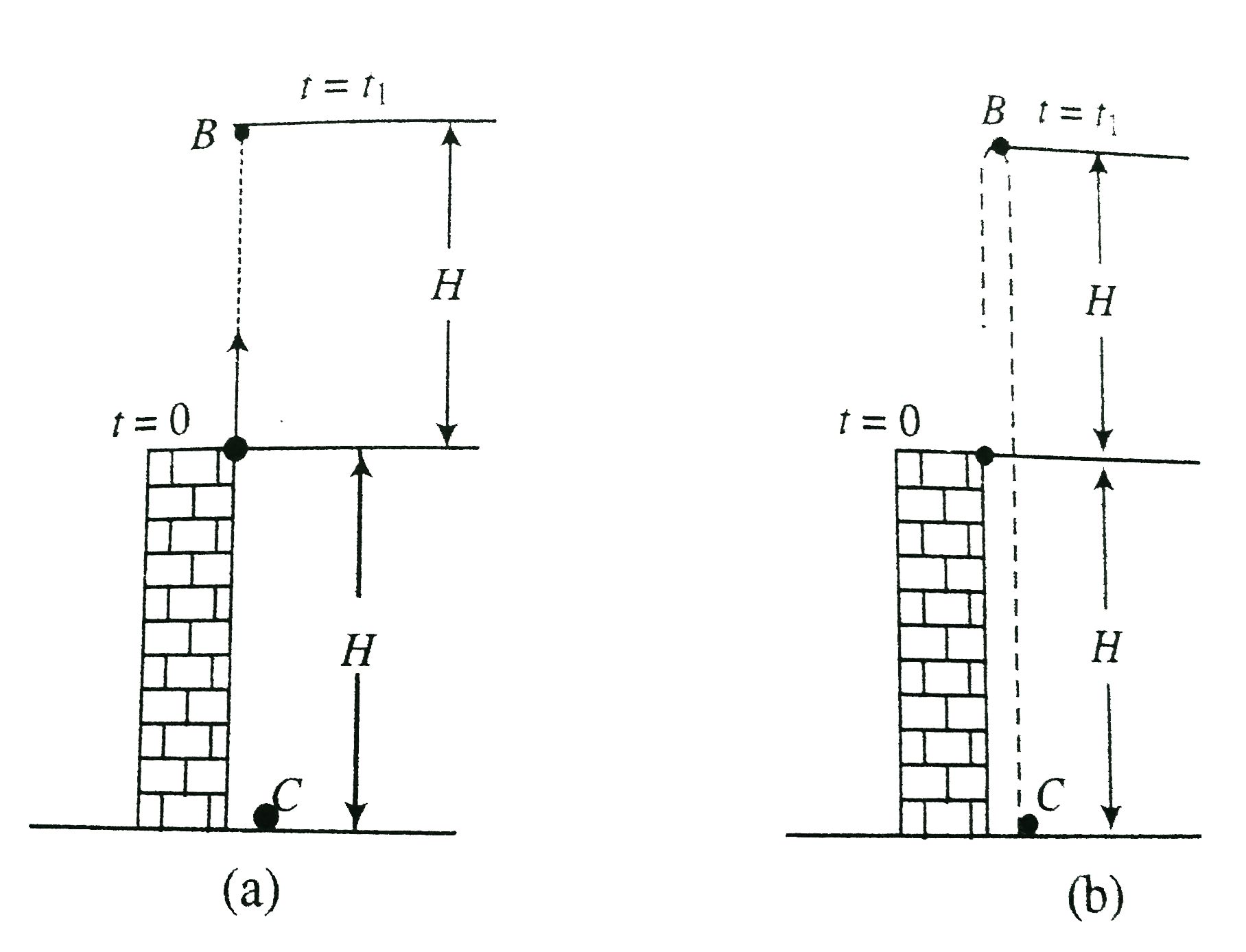
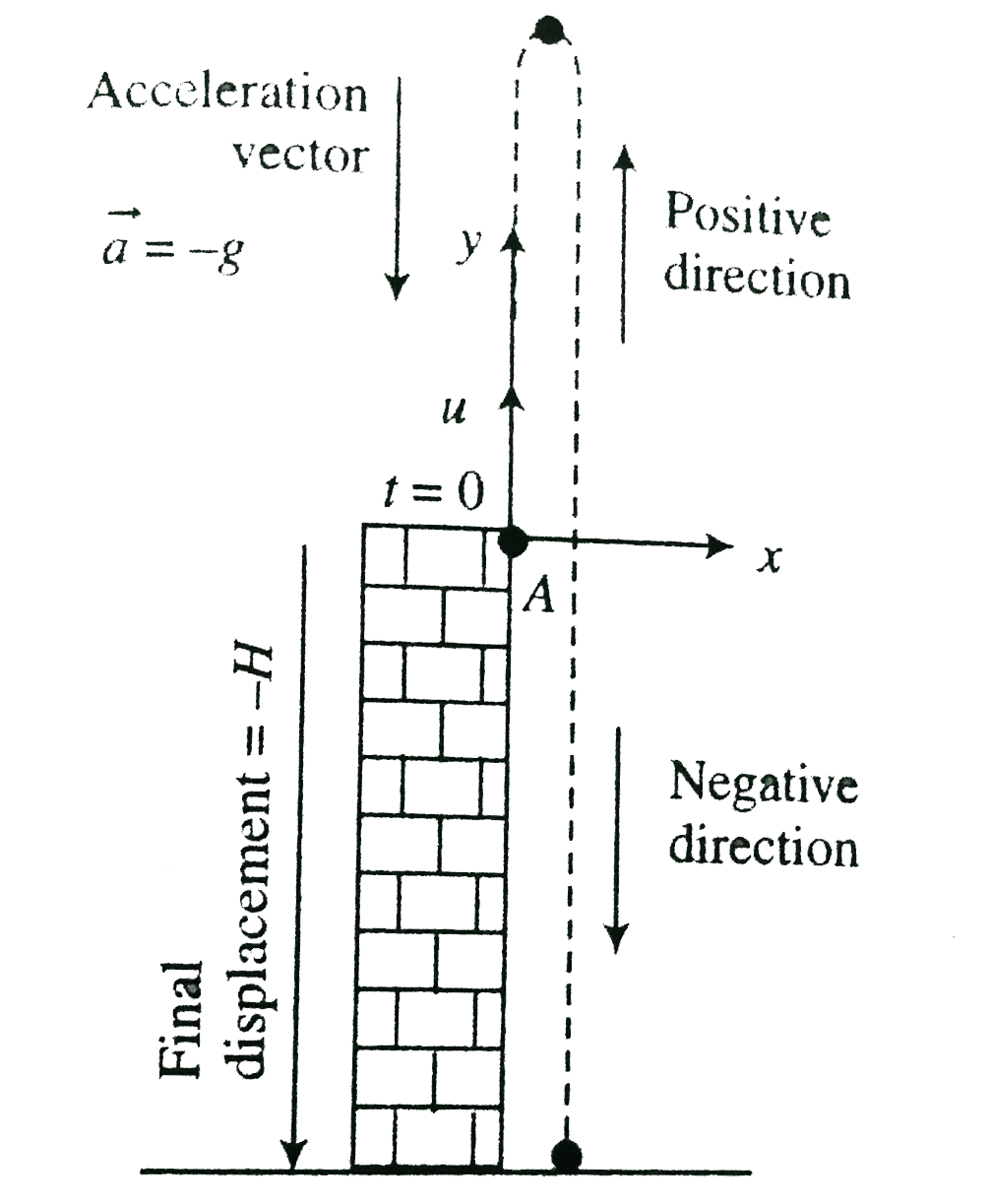
- A particle is projected up with initial speed u=10 m s^(-1) from the t...
Text Solution
|
Playing Now - Form a lift moving upwards with a uniform acceleration a=2 m s^(-2), m...
04:55
|
Play - A train starts from station A with uniform acceleration a(1). For some...
08:45
|
Play - In a car race, car A takes 4 s less than can B at the finish and passe...
04:21
|
Play - A cat, on seeing a rat at a distance d=5 m, starts velocity u=5 m s^(-...
02:59
|
Play - A balloon reses rest on the ground with constant accleeration 1 m s^(-...
06:29
|
Play - A body is thrown up with a velocity 1000 m s^(-1). It travels 5 m in t...
03:34
|
Play - In quick succession, a large number of balls are throun up vertically ...
02:23
|
Play - A police is chasing a culprit going n a motorbike. The motorbike cross...
03:53
|
Play - On a two lane road, car A is travelling with a speed of 36 km h^(-1), ...
05:03
|
Play
 .
.
 .
.