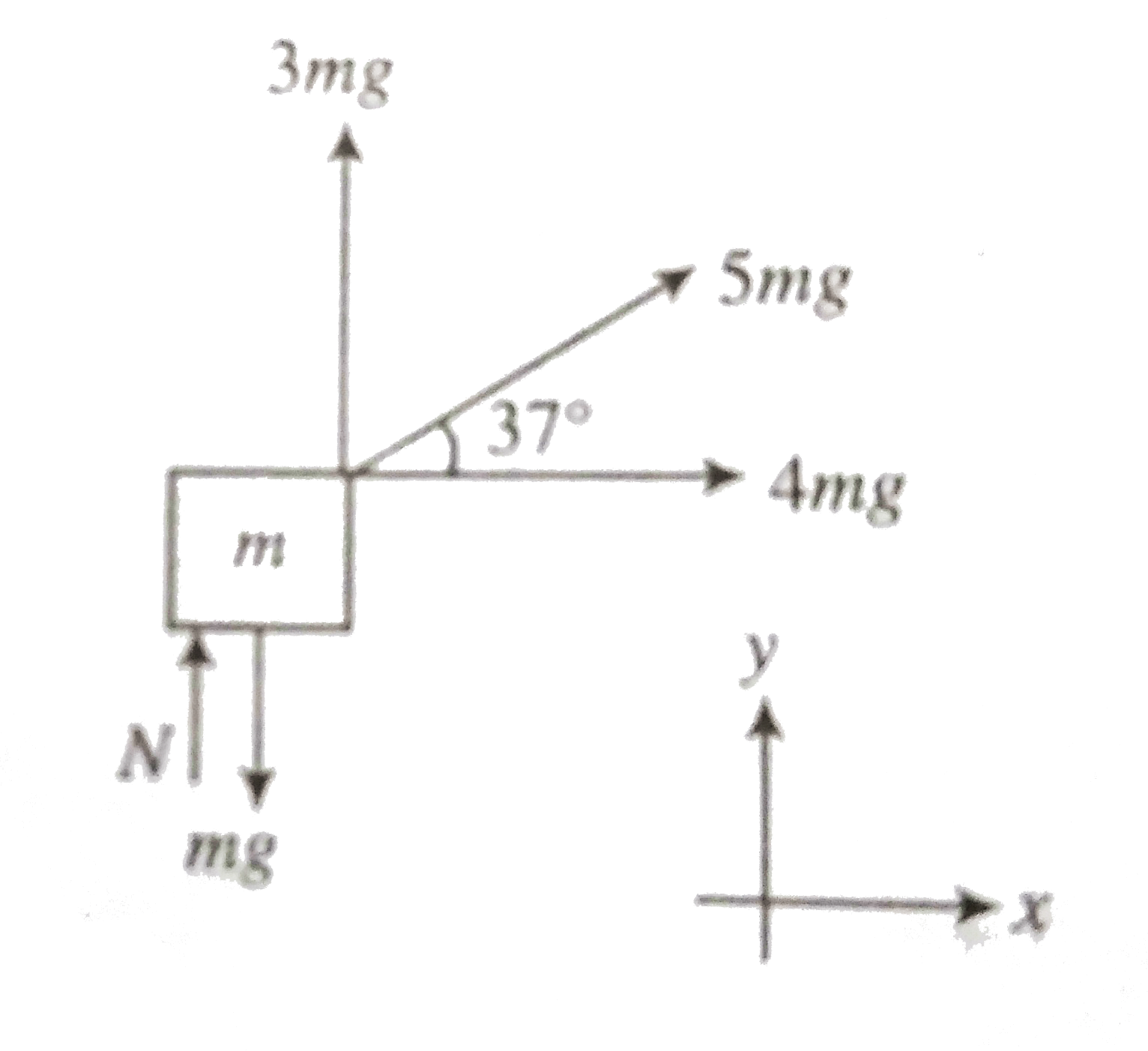
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
NEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Solved Examples|11 VideosView PlaylistNEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Exercise 6.1|11 VideosView PlaylistMISCELLANEOUS VOLUME 2
CENGAGE PHYSICS|Exercise INTEGER_TYPE|10 VideosView PlaylistNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS|Exercise Integer type|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 1-Integer
- A block of mass m is placed on a horizontla surface. If the block is p...
04:08
|
Playing Now - A block is placed on an inclined plane moving towards right horizontal...
07:57
|
Play - You are designing an elevator for a hospital. The force exerted on a p...
03:30
|
Play - Figure represents a painter in a crate which hangs alongside a buildin...
07:08
|
Play - The elevator shown in fig. is descending with an acceleration of 2ms^(...
01:58
|
Play - Block A is given an acceleration 12 ms^(-2) towards left as shown in f...
03:22
|
Play