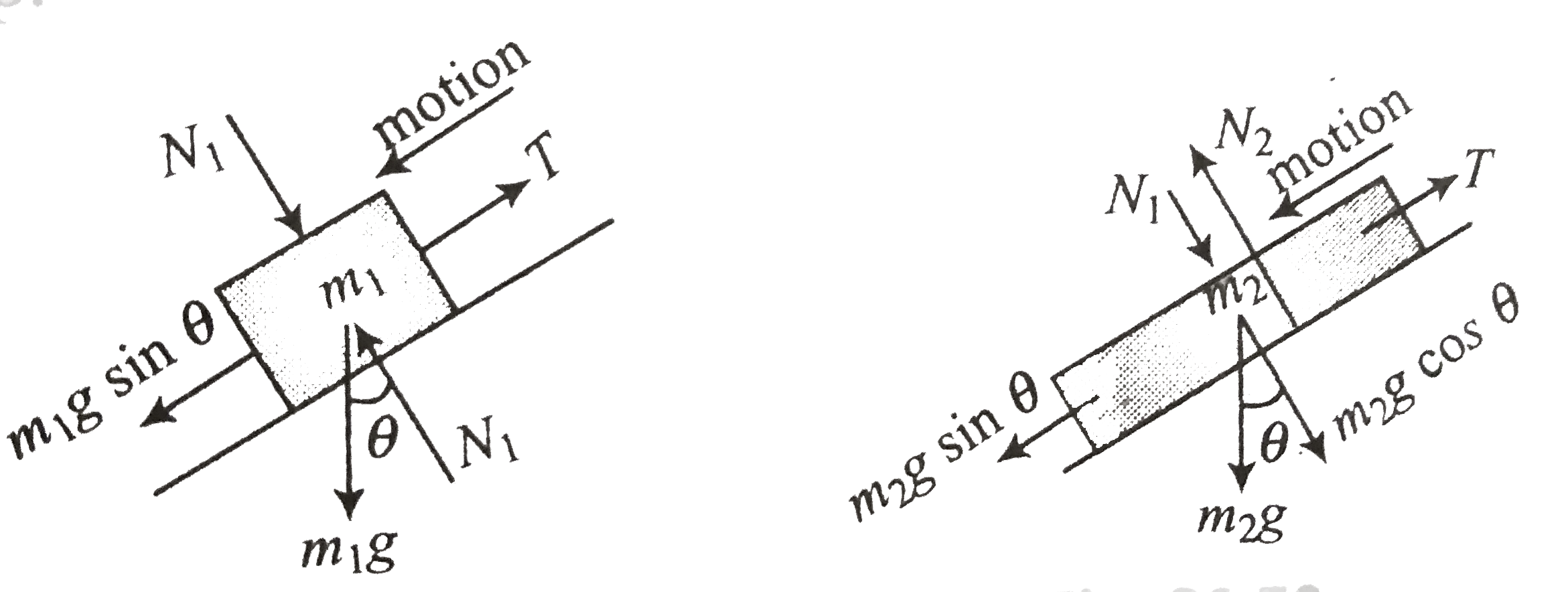Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
NEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Single Correct|76 VideosView PlaylistNEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Multiple Correct|11 VideosView PlaylistNEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Exercise 6.4|13 VideosView PlaylistMISCELLANEOUS VOLUME 2
CENGAGE PHYSICS|Exercise INTEGER_TYPE|10 VideosView PlaylistNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS|Exercise Integer type|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 1-Subjective
- A hot- air balloon consists of a basket, one passenger, and some carge...
03:39
|
Play - A student tries to raise a chain consisting of three identical links. ...
05:18
|
Play - Two men of masses M and M+m start simultaneously from the ground and c...
06:23
|
Play - In fig. the man and the platform together weight 950N. The pulley can ...
02:23
|
Play - The monkey B shown in figure is holding on to the tail of the monkey A...
10:06
|
Play - A smooth ring A of mass m can slide on a fixed horizontal rod. A strin...
11:03
|
Play - A particle A of mass 2m is held on a smooth horizontal table and is at...
08:25
|
Play - A smooth pulley A of mass M(0) is lying on a frictionless table. A mas...
04:22
|
Play - The upper surface of blokc C is horizontal and its right part is incli...
05:58
|
Play - In the arrangement shown in fig., all pulleys are smooth and massless....
10:41
|
Play - Figure shows a block of mass m(1) sliding on a block of mass m(2), wit...
09:05
|
Playing Now - The system shown in fig. is given an acceleration a towards left. Assu...
02:57
|
Play - In the arrangement shown in fig. a wedge of mass m(3) =3.45 kg is plac...
Text Solution
|
Play - In the system shown in fig., m(A)=4m, m(B)=3m, and m(c)=8m. Friction i...
08:26
|
Play - The system shown in fig, is released from rest. Calculate the tension ...
04:09
|
Play