Text Solution
Verified by Experts
|
Topper's Solved these Questions
RIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Subjective|13 VideosView PlaylistRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Single Correct|97 VideosView PlaylistRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Exercise 2.3|15 VideosView PlaylistPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS|Exercise INTEGER_TYPE|2 VideosView PlaylistRIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Interger|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-RIGID BODY DYNAMICS 1-Exercise 2.4
- A uniform rod of mass m and length l can rotate in a vertical plane ab...
02:25
|
Play - A uniform rod of mass m and length l can rotate in a vertical plane ab...
03:06
|
Play - A wheel of radius r and moment of inertia I about its axis is fixed at...
03:04
|
Play - A uniform rod AB of mass m = 2 kg and length l = 1.0 m is placed on a ...
04:07
|
Play - A cotton reel of mass m, radius R and moment of inertia I is kept on a...
01:25
|
Play - Find acceleration a and angular acceleration alpha. If F=2N,m=1 kg and...
01:34
|
Play - Find alpha, a(Q) and the point of zero acceleration when the horizonta...
03:02
|
Play - A uniform solid. cylinder A of mass can freely rotate about a horizont...
02:55
|
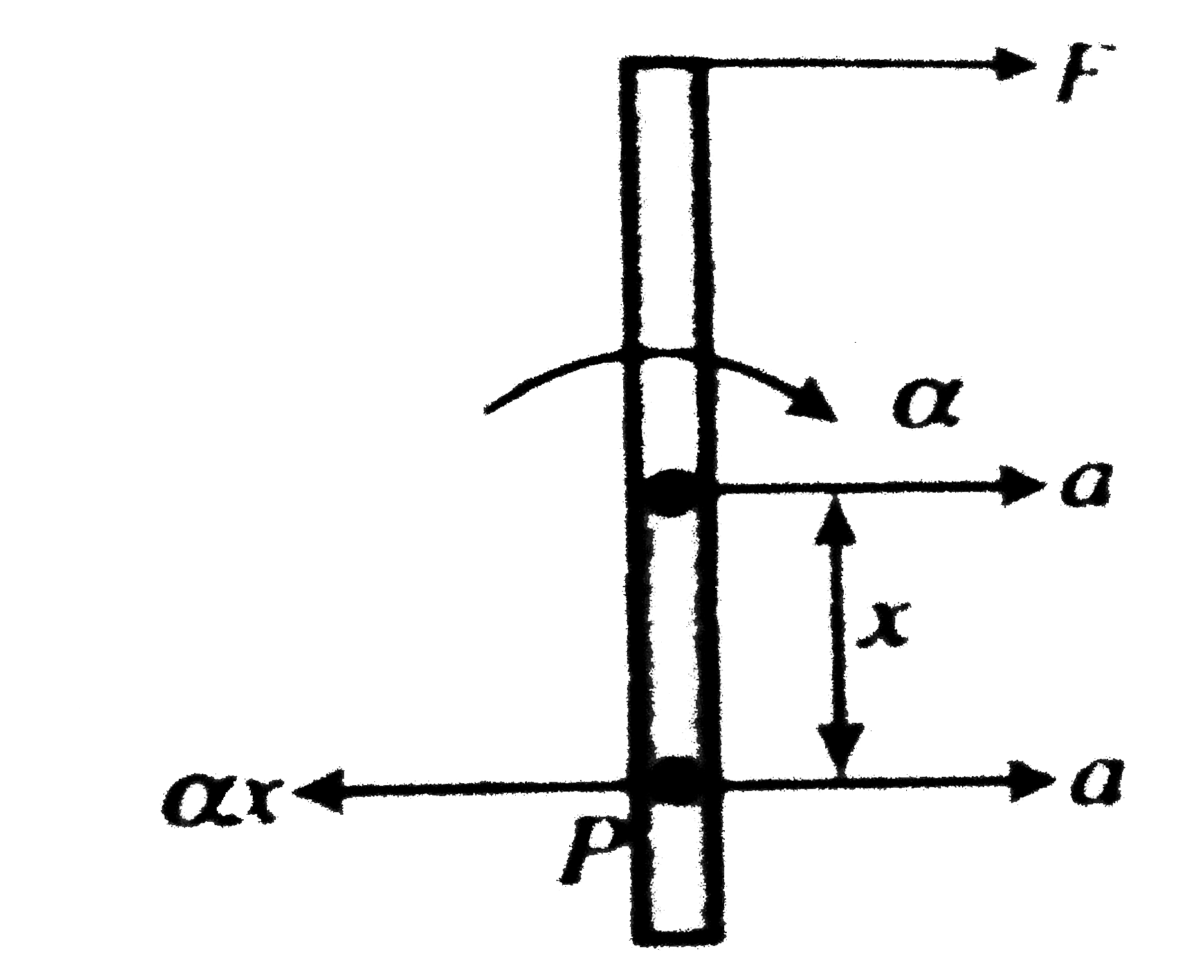
Play - For what value of x, the point P on the rod of length l = 6 m has zero...
02:09
|
Playing Now - A uniform rod of mass m and length is acted upon by the forces F(1) an...
Text Solution
|
Play - Find a(C) and alpha of the smooth rod of mass m and length l.
02:44
|
Play