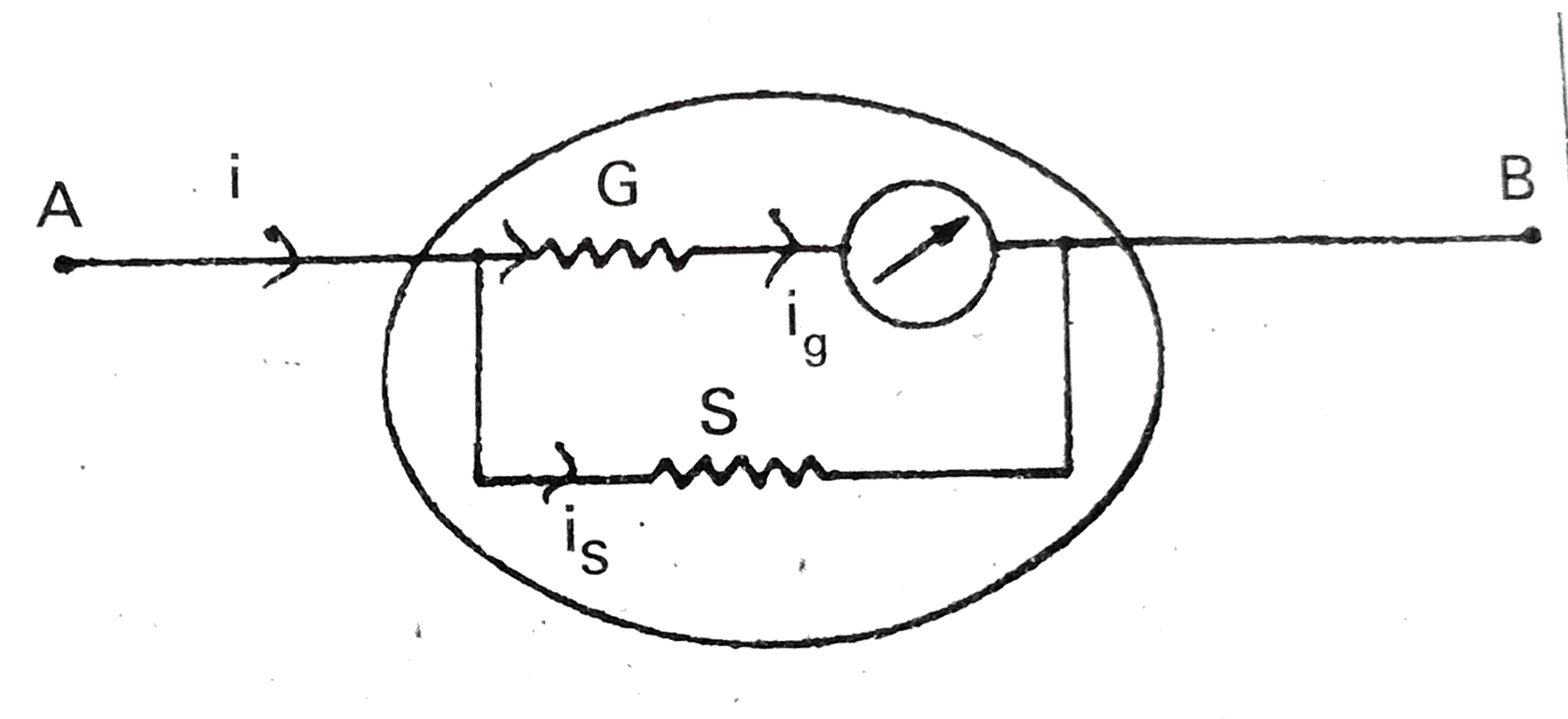
Conversion of Galvanometer into Ammeter : Galvanometer is converted into an ammeter by connecting a suitable resistance is parallel to it. This arrangement decreases the effective resistance. Ammeter is used for measuring the current in an electric circuit and it is connected in series in circuit. The inclusion of the ammeter in the circuit should not alter the current or total resistance of the circuit so it has very low resistance.
The resistance of An ideal Ammeter is zero.
let G and S be the Galvanometer and shunt resistances respectively.
Let 'i' be the total current, divided at A into `i_(g) and i_(s)` as shown in fig. From Kirchhoff's `I^(st)" law "i=i_(g)+i_(s)`
As 'G' and 'S' are parallel P.D. across Galvanometer = P.D. across shunt
`i_(g)G=i_(s)S`
`S=(i_(g))/(i_(s))G`
`=(Gi_(g))/(i-i_(g))" "[because i_(s)=i-i_(g)]`
`S=(G)/((i)/(i_(g))-1)`
If `(i)/(i_(g))= nrArr i_(g)=(i)/(n)`
`therefore` The current flowing through the galvanometer be `((1)/(n))^(h)` of tatal current.
`therefore S=(G)/(n-1)`
If 'R' is the effective resistance between points 'A' and 'B' then
`(1)/(R)=(1)/(G)+(1)/(S)=(S+G)/(GS)`
`R=(GS)/(S+G)`
`iR=i_(s)SrArri_(s)=(i)/(S)R=(i)/(S)((GS)/(S+G))=((G)/(S+G))i`
`i_(s)=((G)/(S+G))i`
Similarly `iR=i_(g)G rArri_(g)=(i)/(G)R=(i)/(G)[(GS)/(S+G)]=((S)/(S+G))i`
`i_(g)=((S)/(S+G))i`
Hence current through galvanometer is proportinal is proportional to the total current. Since 'S' is small major portion of the current flows through it and a small portion of current flows through G. So shunt protects the galvanometer from high currents. Parallel resistance is smaller than Galvanometer resistance because to protect the Galvanometer from high (large) current (or) to pass. Large currents through shunt and small current passes through the galvanometer.
Solution for the problem : Current in the circuit, i=1A,
Current through the galvanometer, `i_(g)=10^(-6)A`
Shunt resistance, `S=(G)/(n-l)=(G)/((i)/(i_(g))-l)=(G)/(l0^(6)-l)=(G)/(99.999)Omega`
