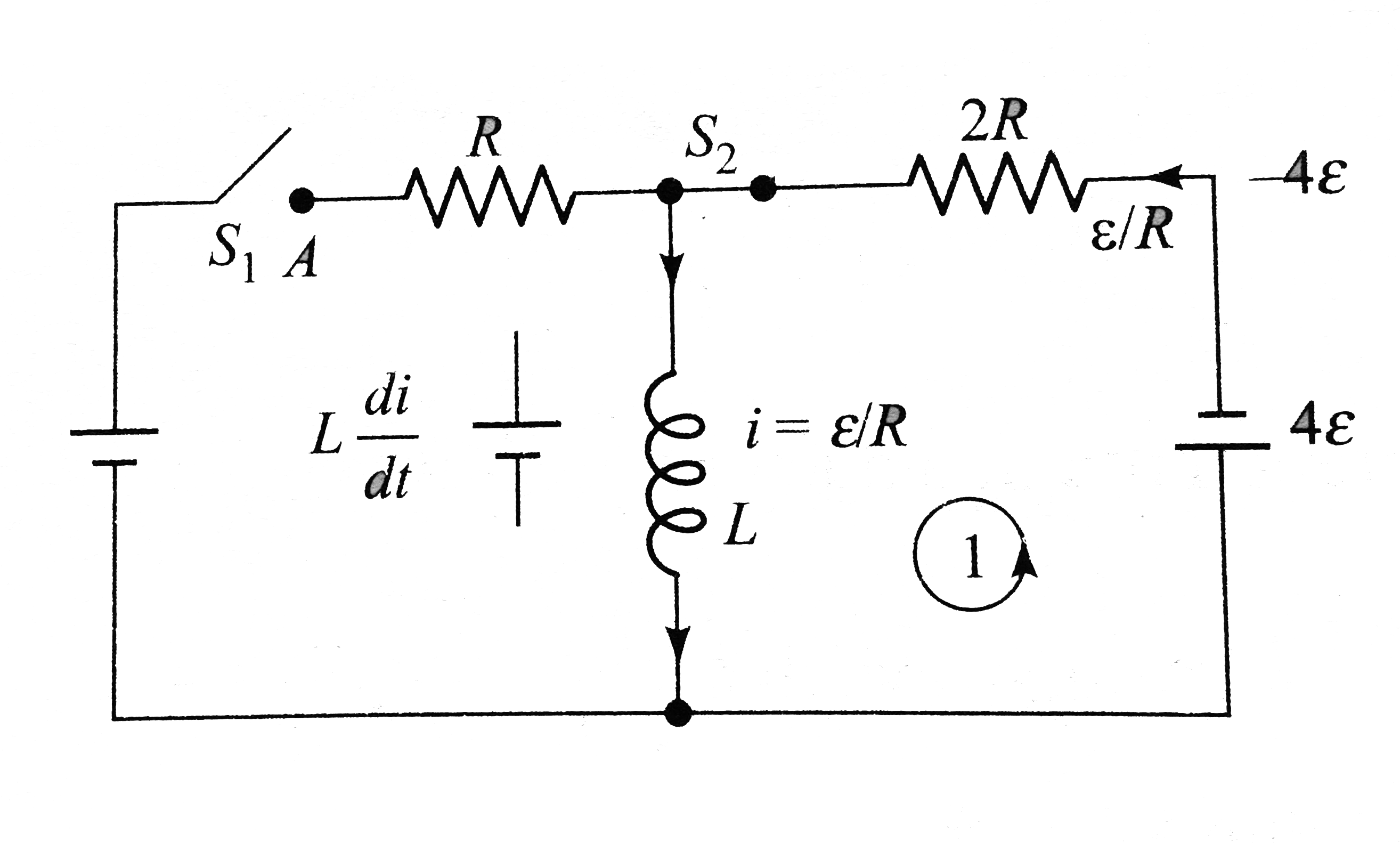Text Solution
Verified by Experts
|
Topper's Solved these Questions
INDUCTANCE
CENGAGE PHYSICS|Exercise Exercises (subjective)|7 VideosView PlaylistINDUCTANCE
CENGAGE PHYSICS|Exercise Exercises (single Correct )|65 VideosView PlaylistINDUCTANCE
CENGAGE PHYSICS|Exercise Solved Examples|3 VideosView PlaylistHEATING EFFECT OF CURRENT
CENGAGE PHYSICS|Exercise Thermal Power in Resistance Connected in Circuit|28 VideosView PlaylistKINETIC THEORY
CENGAGE PHYSICS|Exercise Question Bank|31 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-INDUCTANCE-Exercise 4.1
- Figure shows an LCR circuit. When the switch is closed, the currents t...
00:58
|
Play - It has been proposed to use large inductors as energy storage devices....
01:14
|
Play - A 1 -k Omega resistor is connected in series with a 10-mH inductor, a ...
05:37
|
Play - A capacitor with capacitance 6 xx 10^(-5) F is charged by connecting i...
06:10
|
Play - In the circuit shows in Fig. , E = 10 V, R(1) = 5 Omega, R(2) = 10 Ome...
05:12
|
Play - In Fig. the switch is closed and steady-state conditions are establish...
Text Solution
|
Play - The switch in figure is closed at time t = 0. Find the current in the ...
03:59
|
Play - AB is a part of circuit. Find the potential difference V(A) - V(B) if ...
02:35
|
Play - A circuit contains an ideal cell and an inductor with a switch. Initia...
00:52
|
Play - In the following circuit (Fig.) the switch is closed at t = 0. Find th...
04:54
|
Play - In a circuit S(1) remains closed for a long time and S(2) remain open....
01:35
|
Playing Now - At t = 0, switch S is closed (shown in Fig.). After a long time, sudde...
00:57
|
Play - Which of the two curves shows has lesser time constant.
00:31
|
Play - Two insulated wires are wound on the same hollow cylinder, s as to fro...
01:54
|
Play - Find the mutual inductance of two concentric coils of radii a(1) and a...
01:05
|
Play - Solve problem 19 if the planes of the coils are perpendicular.
00:44
|
Play - Solve problem 19 if the planes of the coils make an angle theta with e...
02:15
|
Play - Figure. shows two concentric coplanar coils with radii a and b(alt lt...
03:16
|
Play - If a capacitor of capacitance C is also connected in the larger loop a...
Text Solution
|
Play - If the current in the inner loop changes according to I = 2t^(2) (Fig ...
Text Solution
|
Play