A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
MISCELLANEOUS VOLUME 5
CENGAGE PHYSICS|Exercise Multiple Correct|34 VideosView PlaylistMISCELLANEOUS VOLUME 5
CENGAGE PHYSICS|Exercise Linked Comprehension|84 VideosView PlaylistMISCELLANEOUS VOLUME 3
CENGAGE PHYSICS|Exercise True and False|3 VideosView PlaylistMoving charges and magnetism
CENGAGE PHYSICS|Exercise Question Bank|20 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-MISCELLANEOUS VOLUME 5-Integer
- A positive charge particle of mass m and charge q is projected with ve...
04:26
|
Playing Now - A charged particle enters a uniform magnetic field with velocity v(0) ...
05:57
|
Play - A charged particle of mass m = 1 mg and charge q = 1 (mu) C enter alon...
02:43
|
Play - Two parallel wires carrying equal currents i(1) and i(2) with i(1)gti(...
04:24
|
Play - A conducting rod of mass 200 gm and length 10 cm can slide without fri...
05:05
|
Play - An infinitely long conductor PQR is bent to form a right angle as show...
04:39
|
Play - A magnetic field vec(B)=-B(0)hat(i) exists within a sphere of radius R...
03:24
|
Play - In the given circuit, what is the current I (in A) drawn from battery ...
04:20
|
Play - A coil of inductance L = 5//8 H and of resistance R = 62.8 (Omega) is ...
05:10
|
Play - In the given LCR series circuit find the reading (in A) of the hot wir...
04:09
|
Play - At any instant a current of 2 A is increasing at a rate of 1 A//s thro...
01:55
|
Play - The diagram shows a circuit having a coil of resistance R = 2.5 (Omega...
04:30
|
Play - A thin wire AC shaped as a semi-circle of diameter d rotates with a co...
Text Solution
|
Play
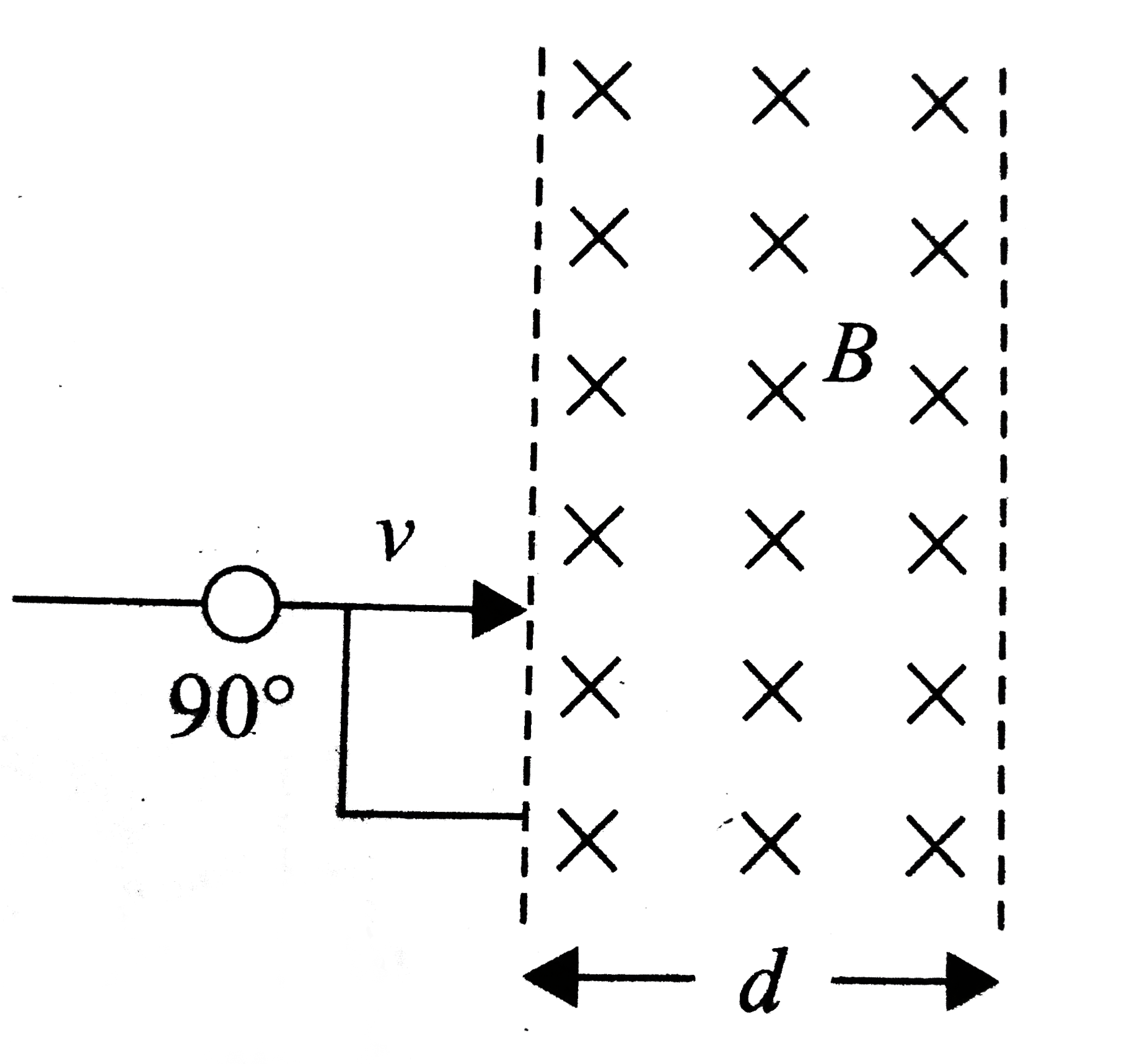
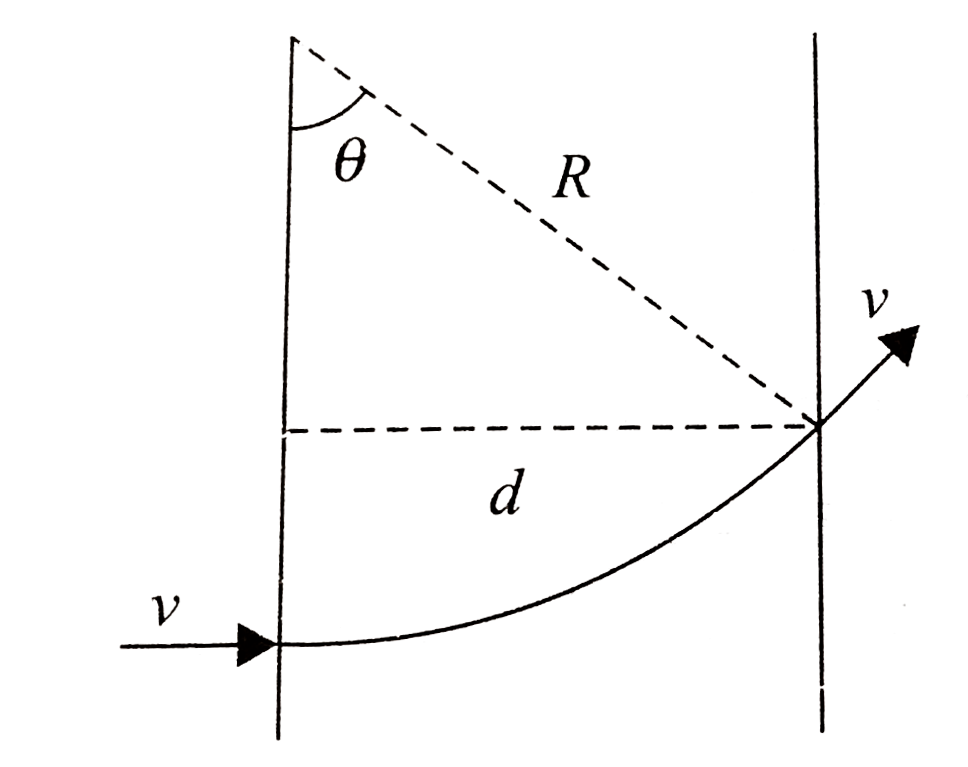 .
.