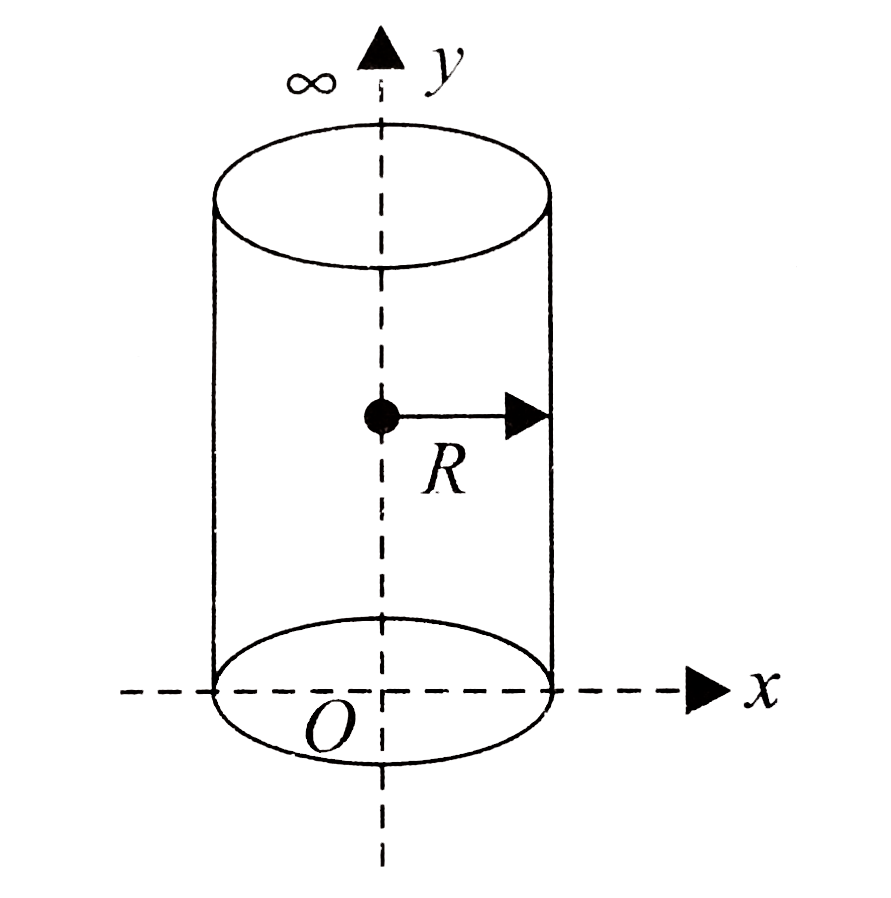A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-MISCELLANEOUS VOLUME 5-Linked Comprehension
- An infinite cylindrical wire of radius R and having current density va...
Text Solution
|
- An infinite cylindrical wire of radius R and having current density va...
Text Solution
|
- An infinite cylindrical wire of radius R and having current density va...
Text Solution
|
- A closed current-carrying loop having a current I is having area A. Ma...
Text Solution
|
- A closed current-carrying loop having a current I is having area A. Ma...
Text Solution
|
- A closed current-carrying loop having a current I is having area A. Ma...
Text Solution
|
- A charged particle with charge to mass ratio ((q)/(m)) = (10)^(3)/(19)...
Text Solution
|
- A charged particle with charge to mass ratio ((q)/(m)) = (10)^(3)/(19)...
Text Solution
|
- A charged particle with charge to mass ratio ((q)/(m)) = (10)^(3)/(19)...
Text Solution
|
- PQRS is a square region of side 2a in the plane of paper. A uniform ma...
Text Solution
|
- PQRS is a square region of side 2a in the plane of paper. A uniform ma...
Text Solution
|
- PQRS is a square region of side 2a in the plane of paper. A uniform ma...
Text Solution
|
- An indcutor having self inductance L with its coil resistance R is con...
Text Solution
|
- An indcutor having self inductance L with its coil resistance R is con...
Text Solution
|
- An indcutor having self inductance L with its coil resistance R is con...
Text Solution
|
- As a charged particle 'q' moving with a velocity vec(v) enters a unifo...
Text Solution
|
- As a charged particle 'q' moving with a velocity vec(v) enters a unifo...
Text Solution
|
- As a charged particle 'q' moving with a velocity vec(v) enters a unifo...
Text Solution
|
- ABCDA is a closed loop of conducting wire consisting of two semicircul...
Text Solution
|
- ABCDA is a closed loop of conducting wire consisting of two semicircul...
Text Solution
|