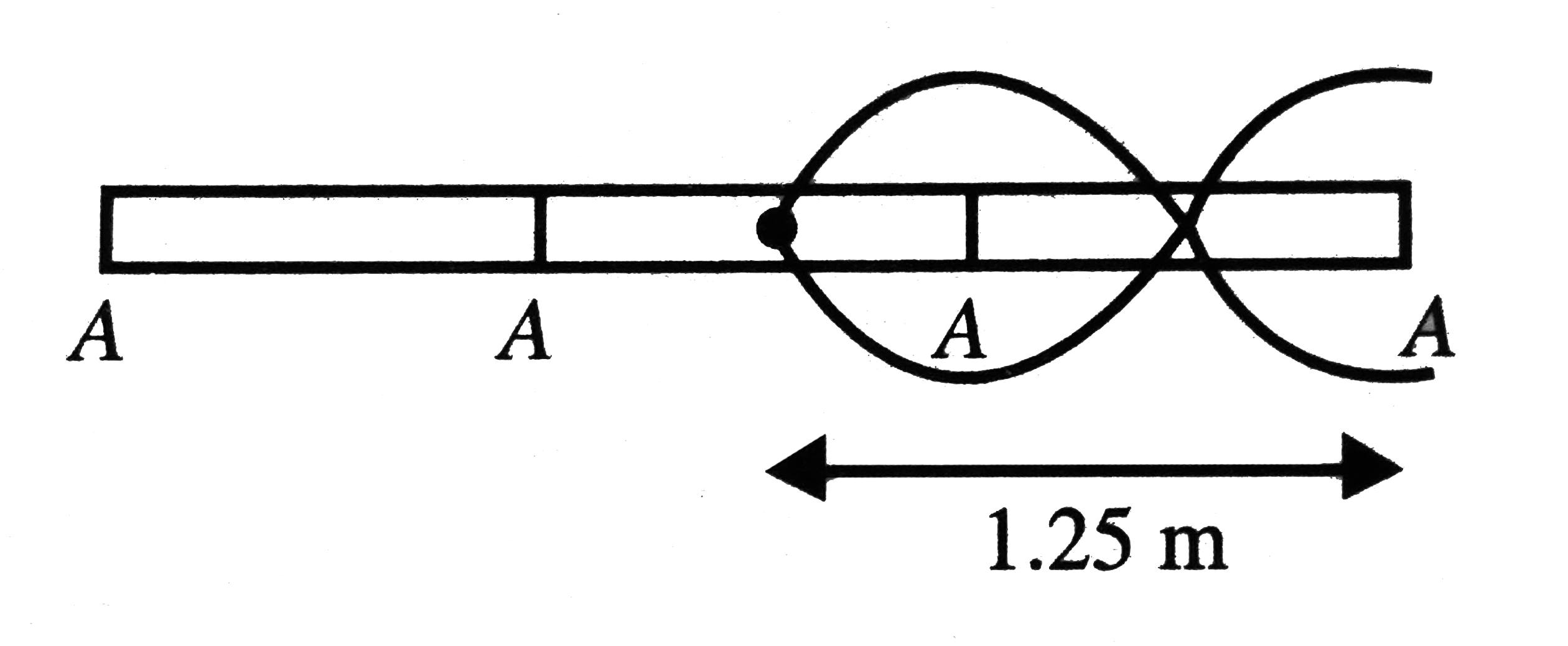
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
SUPERPOSITION AND STANDING WAVES
CENGAGE PHYSICS|Exercise Integer|9 VideosView PlaylistSUPERPOSITION AND STANDING WAVES
CENGAGE PHYSICS|Exercise Multiple Correct Answers Type|5 VideosView PlaylistSUPERPOSITION AND STANDING WAVES
CENGAGE PHYSICS|Exercise Assertion - Reasoning|6 VideosView PlaylistSOUND WAVES AND DOPPLER EFFECT
CENGAGE PHYSICS|Exercise Integer|16 VideosView PlaylistTHERMODYNAMICS
CENGAGE PHYSICS|Exercise 24|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-SUPERPOSITION AND STANDING WAVES-Comprehension
- A long tube contains air at a pressure of 1 atm and a temperature of ...
05:08
|
Play - A long tube contains air at a pressure of 1 atm and a temperature of ...
05:08
|
Play - A steel rod 2.5 m long is rigidly clamped at its centre C and longitud...
04:30
|
Playing Now - A steel rod 2.5 m long is rigidly clamped at its centre C and longitud...
05:47
|
Play - A steel rod 2.5 m long is rigidly clamped at its centre C and longitud...
03:44
|
Play - A longitudinal standing wave y = a cos kx cos omega t is maintained i...
08:12
|
Play - A longitudinal standing wave y = a cos kx cos omega t is maintained i...
08:12
|
Play - A longitudinal standing wave y = a cos kx cos omega t is maintained i...
08:12
|
Play - In a standing wave experiment , a 1.2 - kg horizontal rope is fixed in...
03:25
|
Play - In a standing wave experiment , a 1.2 - kg horizontal rope is fixed in...
07:05
|
Play - In a standing wave experiment , a 1.2 - kg horizontal rope is fixed in...
Text Solution
|
Play - In an organ pipe (may be closed or open ) of 99 cm length standing wav...
06:05
|
Play - In an organ pipe ( may be closed or open of 99 cm length standing wave...
06:03
|
Play - In an organ pipe (may be closed or open ) of 99 cm length standing wav...
03:20
|
Play - Assume end correction approximately equals to (0.3) xx (diameter of tu...
02:01
|
Play - Two plane harmonic sound waves are expressed by the equations. y(1)(...
08:56
|
Play - Two waves y(1) = A cos (0.5 pi x - 100 pi t) and y(2) = A cos (0.46 pi...
02:36
|
Play - Two waves y(1) = A cos (0.5 pi x - 100 pi t) and y(2) = A cos (0.46 pi...
02:36
|
Play - An oscillator of frequency 680 Hz drives two speakers . The speakers a...
13:26
|
Play - An oscillator of frequency 680 Hz drives two speakers . The speakers a...
13:26
|
Play