Home
Class 11
PHYSICS
A particle of mass m is released from re...

A particle of mass `m` is released from rest from point `P` at `x = x_(0)` on X-axis from origin `O` and falls vertically along y-axis as shown in Fig. What is the magnitude of the torque acting on the particle at time `t`, when it is at the point `Q w.r.t.O` ?

Text Solution

Verified by Experts

Refer to Fig.
Magnitude of torque is
`tau = r F sin theta = r xx mg xx (x_(0))/(r ) = mg x_(0)`
Promotional Banner

Topper's Solved these Questions

  • SYSTEMS OF PARTICLES AND ROTATIONAL MOTION

    PRADEEP|Exercise PROBLEMS FOR PRACTICE TYPE B|2 Videos

  • SYSTEMS OF PARTICLES AND ROTATIONAL MOTION

    PRADEEP|Exercise PROBLEMS FOR PRACTICE TYPE C|2 Videos

  • SYSTEMS OF PARTICLES AND ROTATIONAL MOTION

    PRADEEP|Exercise PROBLEMS FOR PRACTICE TYPE A|2 Videos

  • RAY OPTICS

    PRADEEP|Exercise Problem For Practice(a)|25 Videos

  • THERMODYNAMICS

    PRADEEP|Exercise Assertion- Reason Type Questions|19 Videos

Similar Questions

Explore conceptually related problems

A particle of mass m is released in vertical plane from a point P at x=x_(0) on the x -axis. It falls vertically parallel to the y -axis. Find the torque tau acting on the particle at a time about origin.

In Fig. 10-73, a particle of mass m is released from rest at point A, at distance b from the origin, and falls parallel to a vertical y axis. As a function of time t and with respect to the origin, find the magnitudes of (a) the torque tau on the particle due to the gravitational force and (b) the angular momentum L of the particle. ( c) From those results, verify that tau=dL//dt .

A particle of mass m is released from rest at point A in the figure falling freely under gravity parallel to the vertical Y -axis. The magnitude of angular momentum of particle about point O when it reaches B is (where OA=b and AB=h )

A particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y -axis. Find the angular momentum of the particle at any time t with respect to the same origin O .

v_(x) is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?

A point particle of mass m is released from a distance sqrt(3)R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

V_(x) is the velocity of a particle of a particle moving along the x- axis as shown. If x=2.0m at t=1.0s , what is the position of the particle at t=6.0s ?

A particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

A small particle of mass m is projected at an angle theta with x-axis with initial velocity upsilon_(0) in x-y plane as shown in Fig. Calculate the momentum of the particle at t lt (upsilon_(0) sin theta)/(g) .

A particle of mass m is projected from origin O with speed u at an angle theta with positive x-axis. Positive y-axis is in vertically upward. Direction. Find the angular momentum of particle at any time t about O before the particle strkes the ground again.

PRADEEP-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-PROBLEMS FOR PRACTICE
  1. A flywheel of mass 25 kg has a radius of 0.2 m. It is making 240 rpm. ...

    Text Solution

    |

  2. A rope is wound round a hollow cylinder of mass 3 kg and radius 40 cm....

    Text Solution

    |

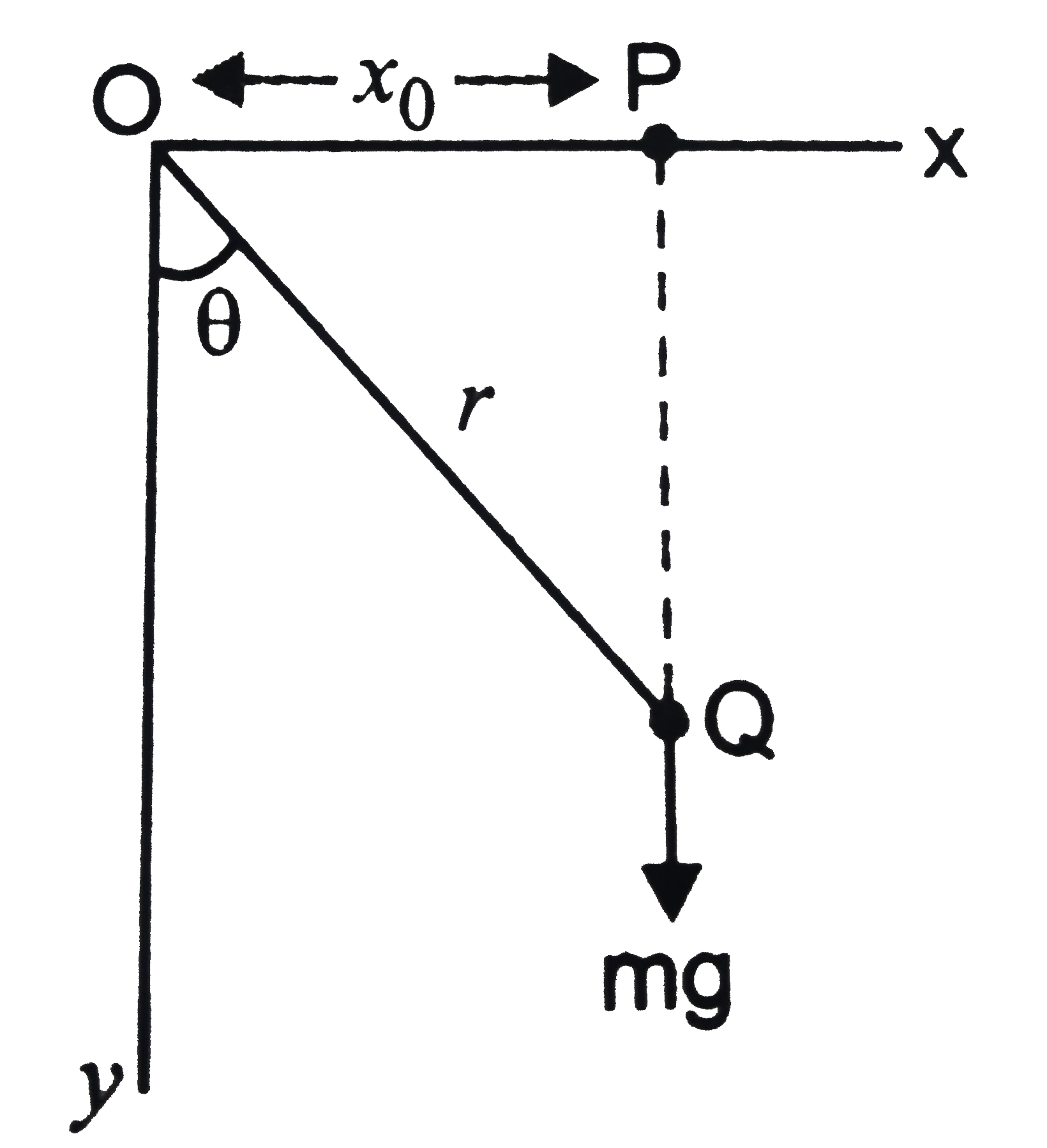
  3. A particle of mass m is released from rest from point P at x = x(0) on...

    Text Solution

    |

  4. A unifrom circular disc of mass 200g and radius 4 cm is rotated about ...

    Text Solution

    |

  5. Determine the angular momentum of a car of mass 200 kg moving in a cir...

    Text Solution

    |

  6. An electron revolves around the nucleus of an atom in a circular orbit...

    Text Solution

    |

  7. Suppose earth is a point mass of 6 xx 10^(24) kg revolving around the ...

    Text Solution

    |

  8. The body shown in Fig. is pivoted at point O. Three forces act on it F...

    Text Solution

    |

  9. The speed of a wheel increases from 600 rpm to 1200 rpm in 20 s. What ...

    Text Solution

    |

  10. A flywheel rotating at 420 rpm slows sown at a constant rate 2 rad s^(...

    Text Solution

    |

  11. The spin drier of a washing machine revolving at15 rps slows down to 5...

    Text Solution

    |

  12. On applying a consatnt torque, a wheel at rest, turns through 400 radi...

    Text Solution

    |

  13. A cord is wound around the circumference of a bicycle wheel (without t...

    Text Solution

    |

  14. A car is moving at a speed of 72 km//h. The diamter of its whells is 0...

    Text Solution

    |

  15. An autmobile travelling at 80 km//h has tyres of 75.0 cm diameter. Wha...

    Text Solution

    |

  16. A wheel rotating at an angular speed of 20 rad/s ils brought to rest b...

    Text Solution

    |

  17. The centre of gravity of a loaded texi is 1.5 m above the ground, and ...

    Text Solution

    |

  18. Calculate rotational K.E. of earth about its own axis, taking it to be...

    Text Solution

    |

  19. A wheel of mass 5 kg and radius 0.40 m is rolling on a road without sl...

    Text Solution

    |

  20. A thin metal hoop of radius 0.25 m and mass 2 kg stars from rest and r...

    Text Solution

    |