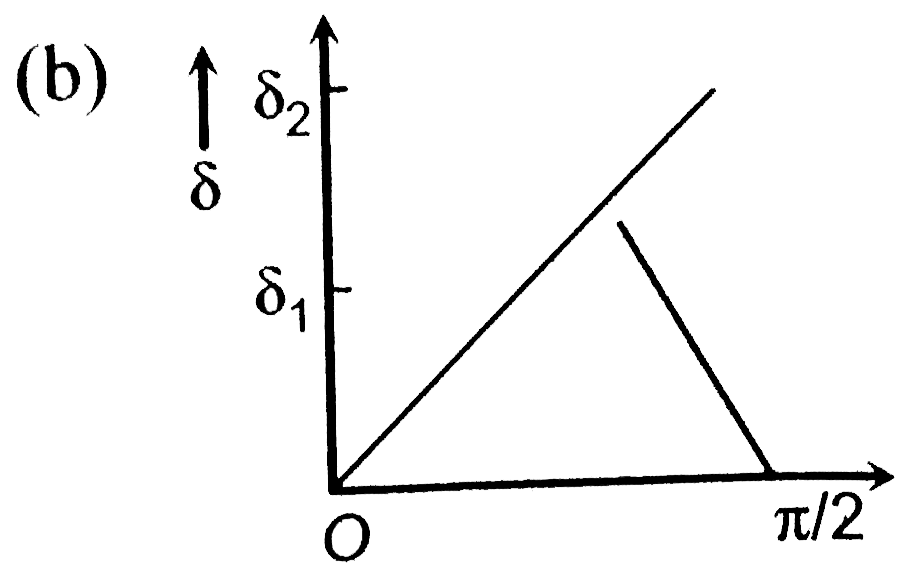
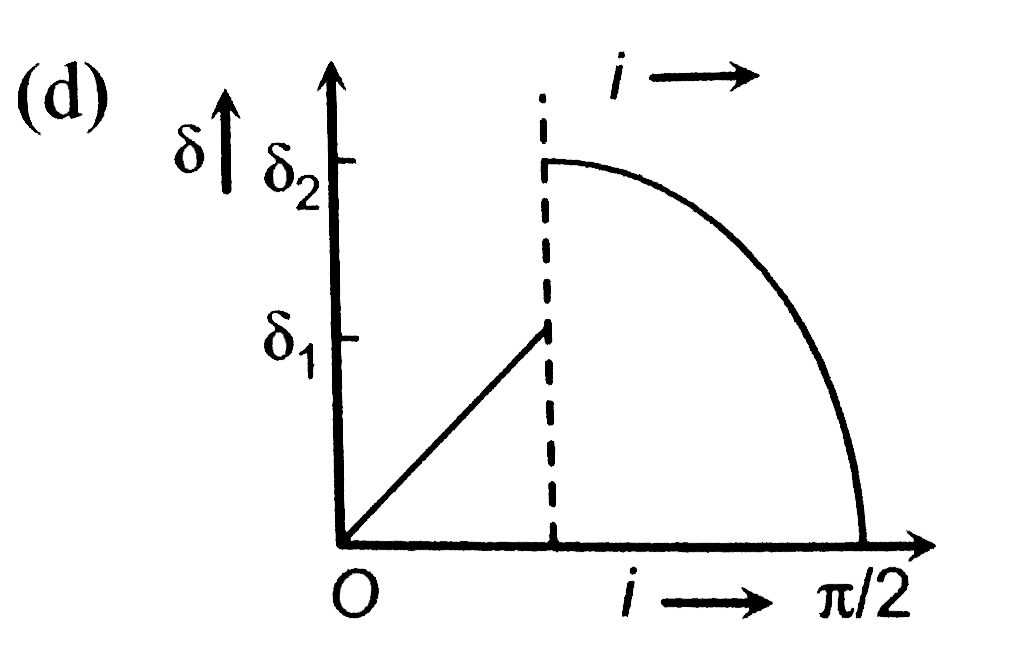
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
GEOMETRICAL OPTICS
A2Z|Exercise Refraction At Curved Surface|64 VideosView PlaylistGEOMETRICAL OPTICS
A2Z|Exercise Prism Theory And Dispersion Of Light|45 VideosView PlaylistELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM
A2Z|Exercise Section D - Chapter End Test|30 VideosView PlaylistMAGNETISM AND MATTER
A2Z|Exercise Section D - Chapter End Test|30 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
A2Z-GEOMETRICAL OPTICS-Section D - Chapter End Test
- A ray of light travels from a medium of refractive index mu to air. It...
05:46
|
Playing Now - Wavelength of light used in an optical instrument are lambda(1)=400 Å ...
02:05
|
Play - A plano convex lens of refractive index 1.5 and radius of curvature 30...
05:18
|
Play - A light ray is incident perpendicularly to one face of a 90^circ prism...
01:10
|
Play - A thin glass (refractive index 1.5) lens has optical power of -5D in a...
03:20
|
Play - Which of the following graphs is the magnification of a real image aga...
02:28
|
Play - A thin prism P(1) with angle 4degree and made from glass of refractive...
01:39
|
Play - A converging lens is used to form an image on a screen. When the upper...
02:23
|
Play - A diminished image of an object is to be obtained on a screen 1.0 m fr...
03:42
|
Play - An object 15cm high is placed 10cm from the optical center of a thin l...
01:03
|
Play - A lens forms a virtual, diminished image of an object placed at 2 m fr...
02:14
|
Play - When the distance between the object and the screen is more than 4 f....
04:10
|
Play - a convex lens of power +6 diopter is placed in contact with a concave ...
01:46
|
Play - A concave lens of focal length 20 cm product an image half in size of ...
03:45
|
Play - A convex lens of focal length 1.0m and a concave lens of focal length ...
01:36
|
Play - If in a planoconvex lens, the radius of curvature of the convex surfac...
02:22
|
Play - A convex lens A of focal length 20cm and a concave lens G of focal le...
01:54
|
Play - The radii of curvature of the two surfaces of a lens are 20cm and 30 c...
03:12
|
Play - A lens forms a virtual image 4 cm away from it when an object is place...
02:42
|
Play - A concave lens of focal length (1)/(3)m forms a real, inverted image t...
03:00
|
Play - An object is placed at a distance of f//2 from a convex lens. The imag...
03:11
|
Play